ETC3250/5250 Introduction to Machine Learning

Week 2: Visualising your data and models

Professor Di Cook

etc3250.clayton-x@monash.edu

Department of Econometrics and Business Statistics

Overview

In this week we will cover:

• Conceptual framing for visualisation
• Common methods: scatterplot matrix, parallel coordinates, tours
• Details on using tours for examining clustering and class structure
• Dimension reduction
  • Linear: principal component analysis
  • Non-linear: multidimensional scaling, t-stochastic neighbour embedding (t-SNE), uniform manifold approximation and projection (UMAP)
• Using tours to assess dimension reduction

Concepts

Model-in-the-data-space

From XKCD

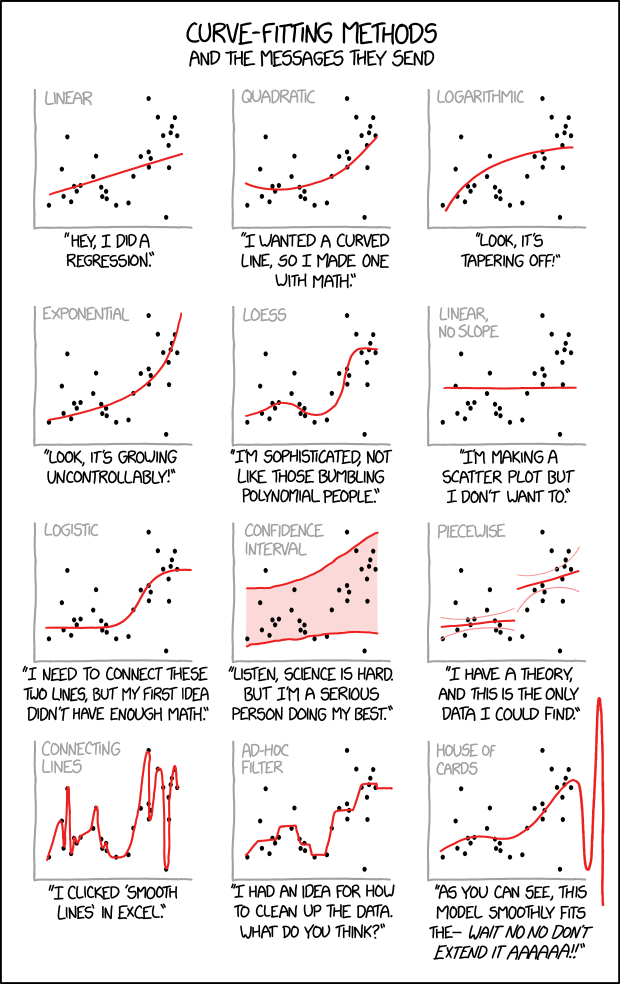
We plot the model on the data to assess whether it fits or is a misfit!

Doing this in high-dimensions is considered difficult!

So it is common to only plot the data-in-the-model-space.

Data-in-the-model-space

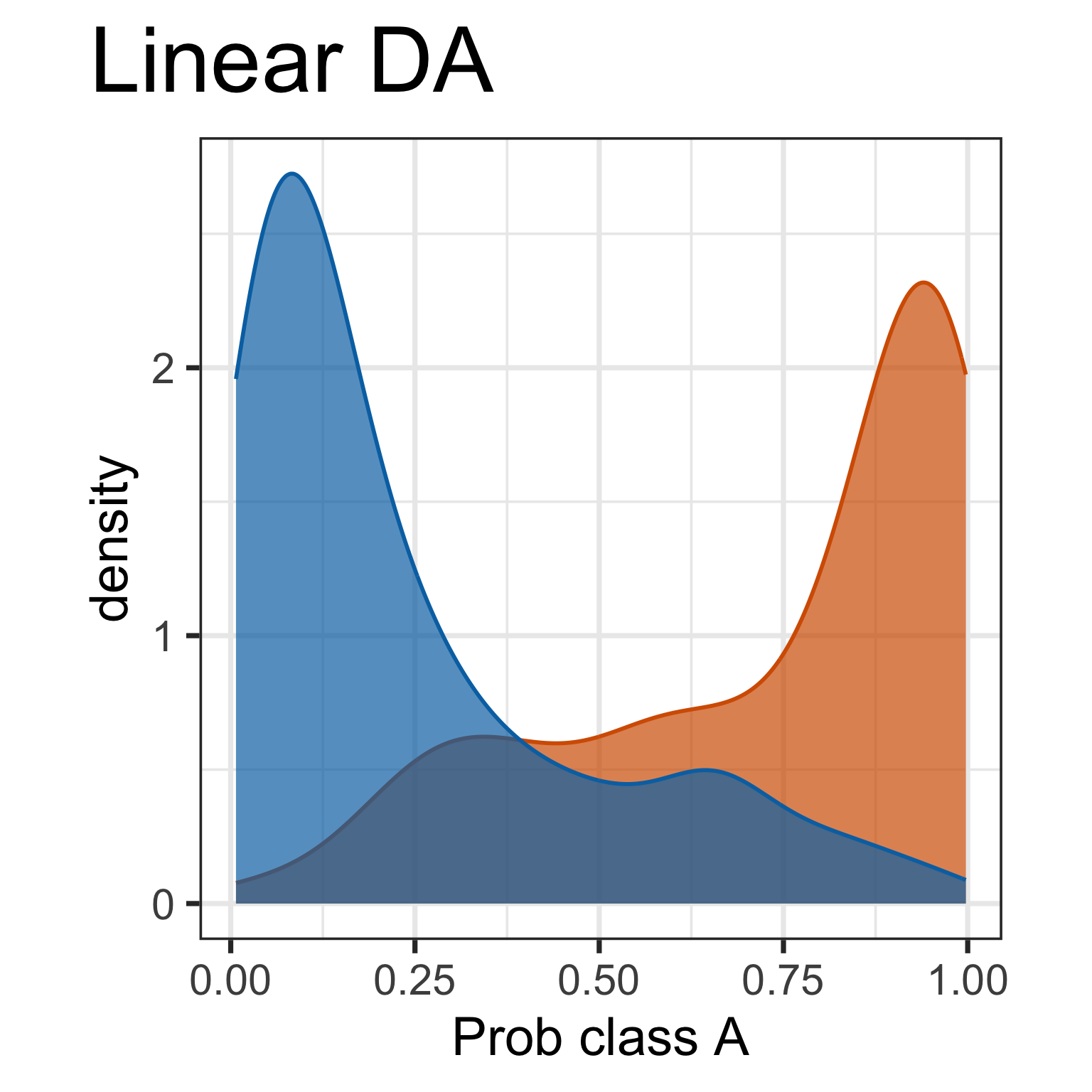
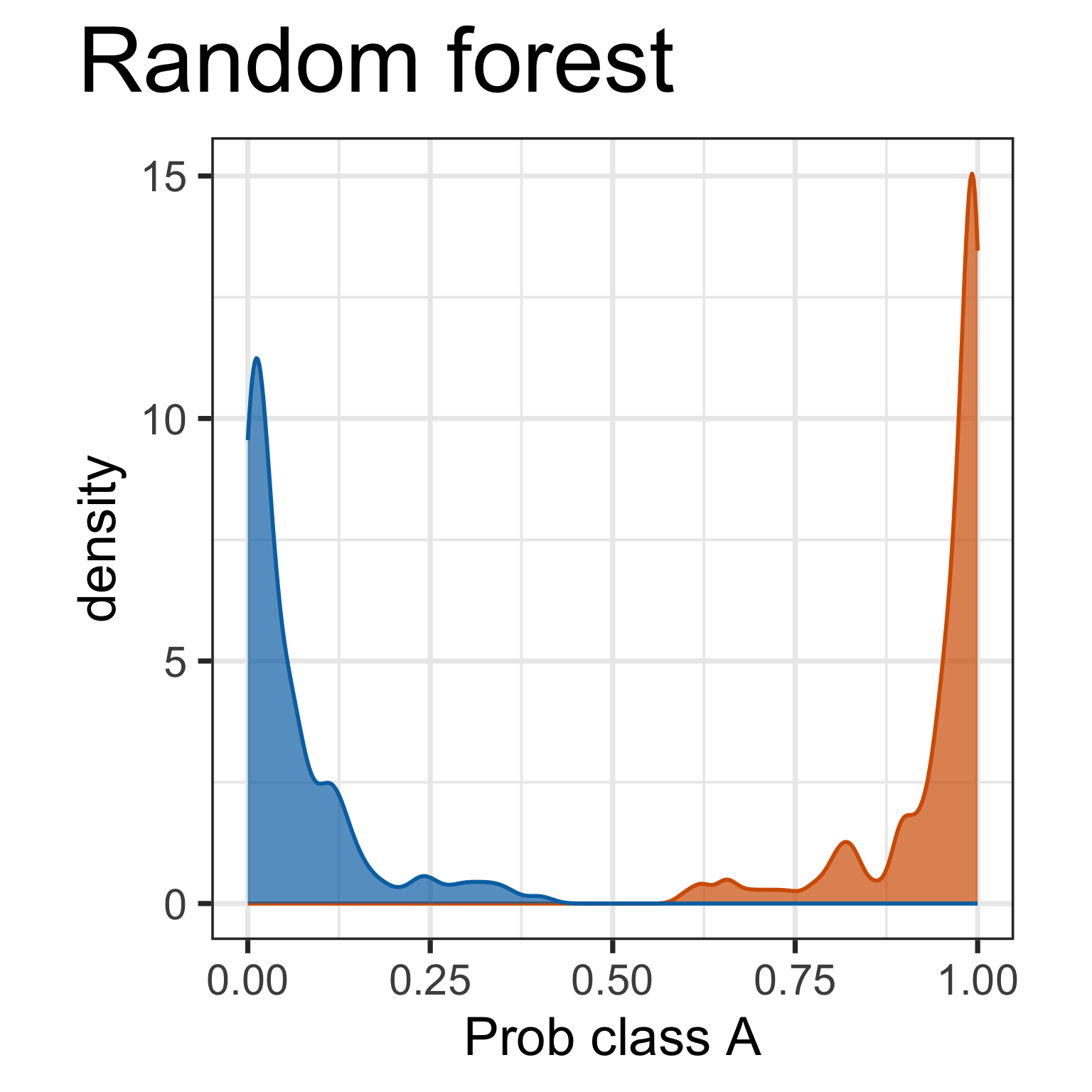
Predictive probabilities are aspects of the model. It is useful to plot. What do we learn here?

But it doesn’t tell you why there is a difference.

Model-in-the-data-space

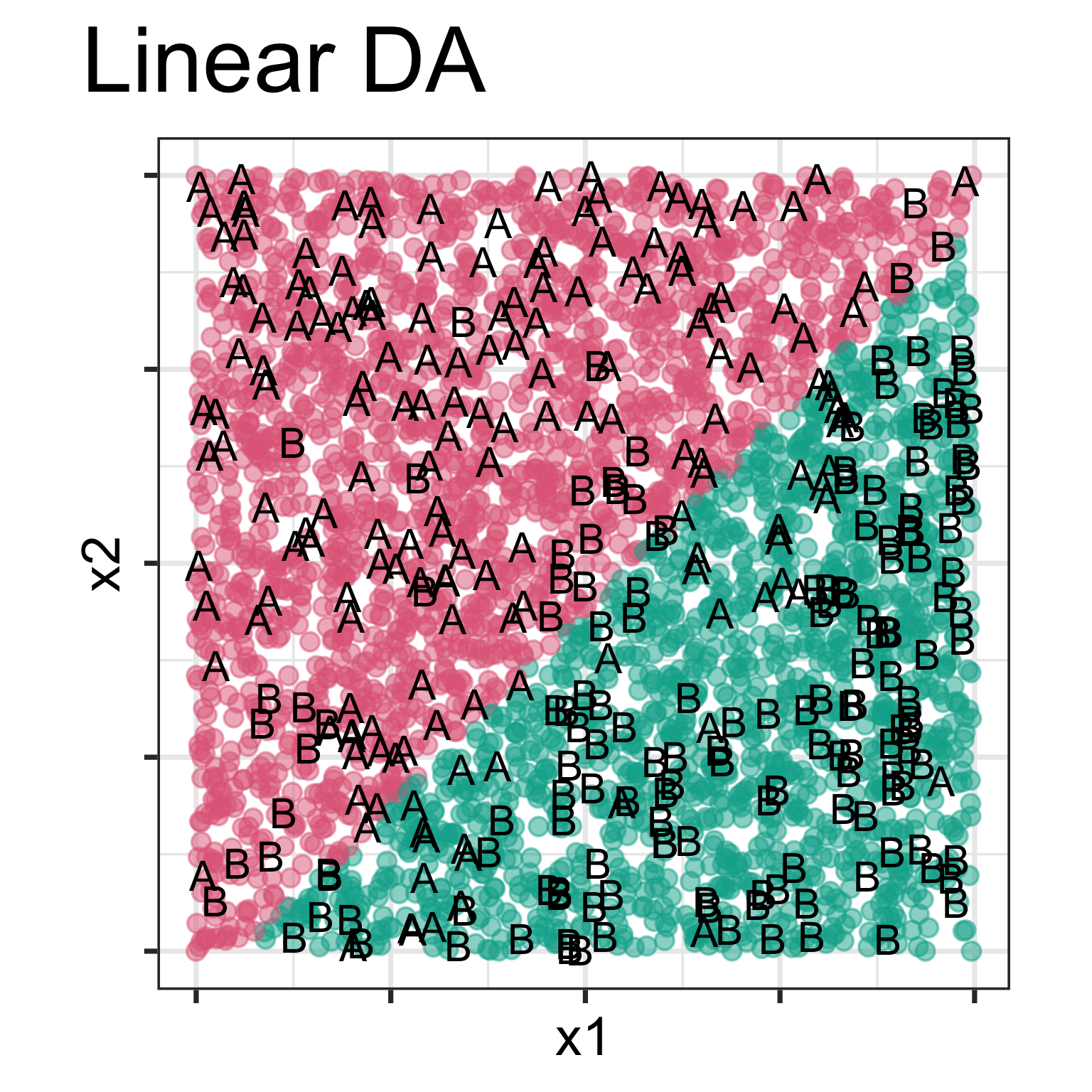
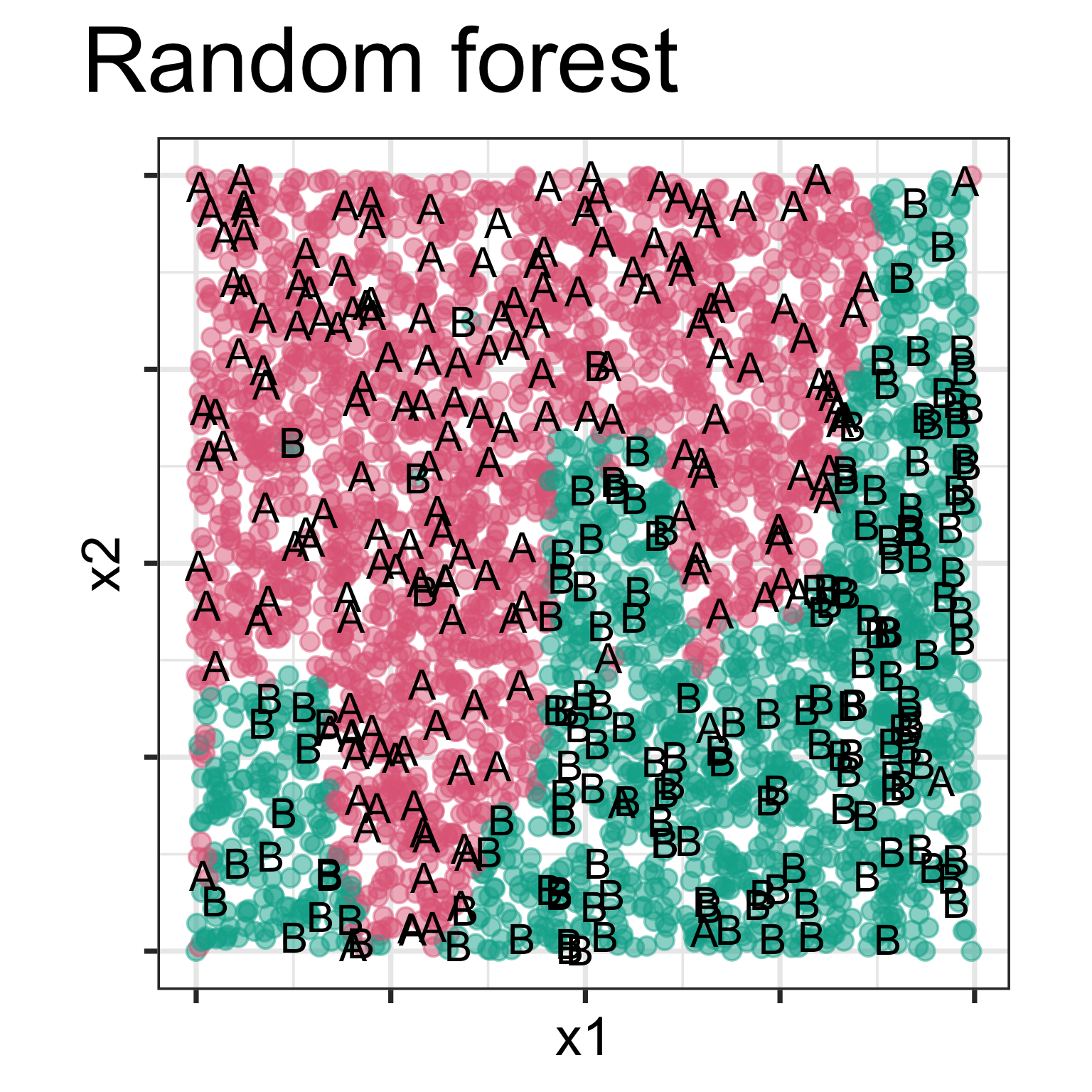
Model is displayed, as a grid of predicted points in the original variable space. Data is overlaid, using text labels. What do you learn?

One model has a linear boundary, and the other has the highly non-linear boundary, which matches the class cluster better. Also …

How do you visualise beyond 2D?

Scatterplot matrix

Start simply! Make static plots that organise the variables on a page.

Plot all the pairs of variables. When laid out in a matrix format this is called a scatterplot matrix.

Here, we see linear association, clumping and clustering, potentially some outliers.

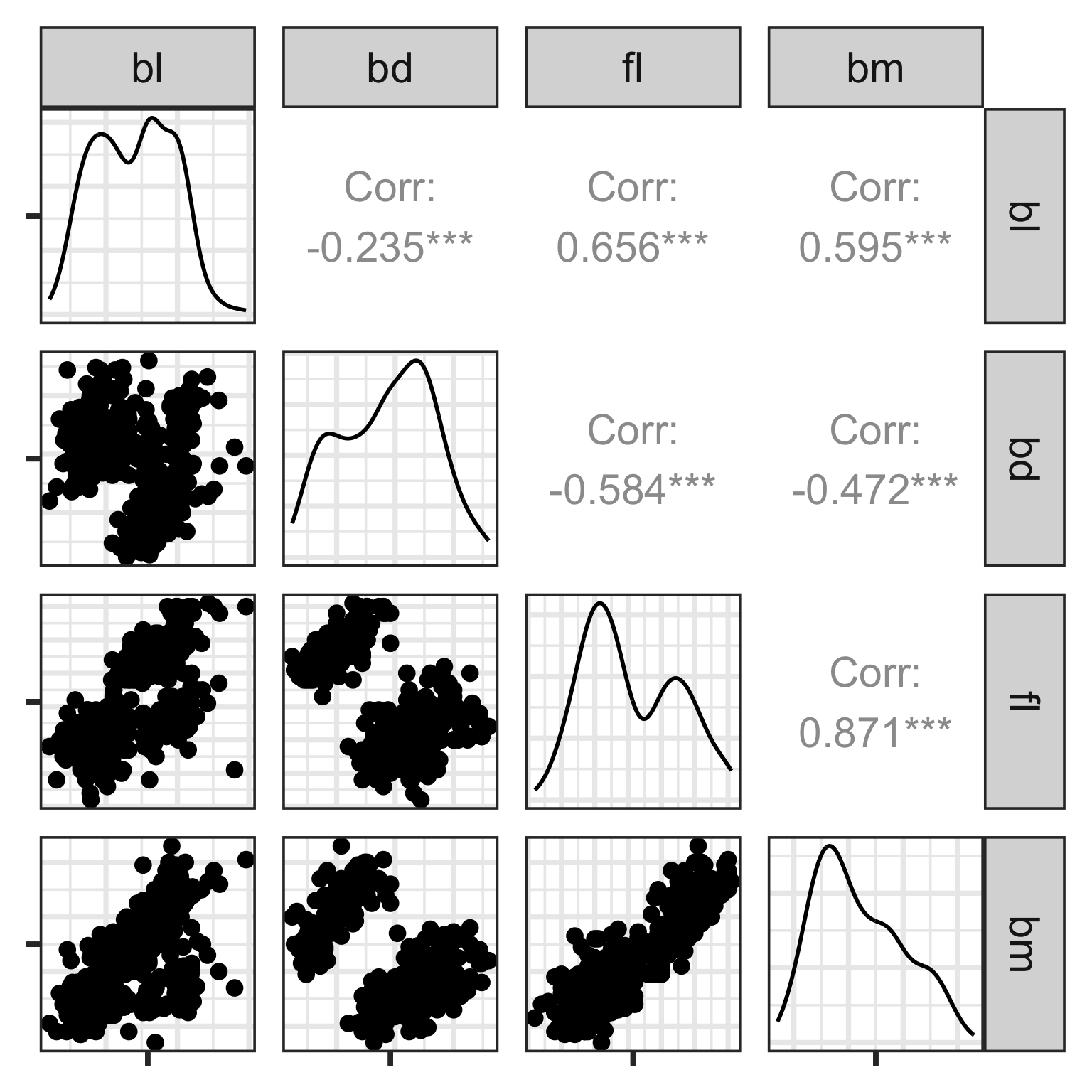
Scatterplot matrix: drawbacks

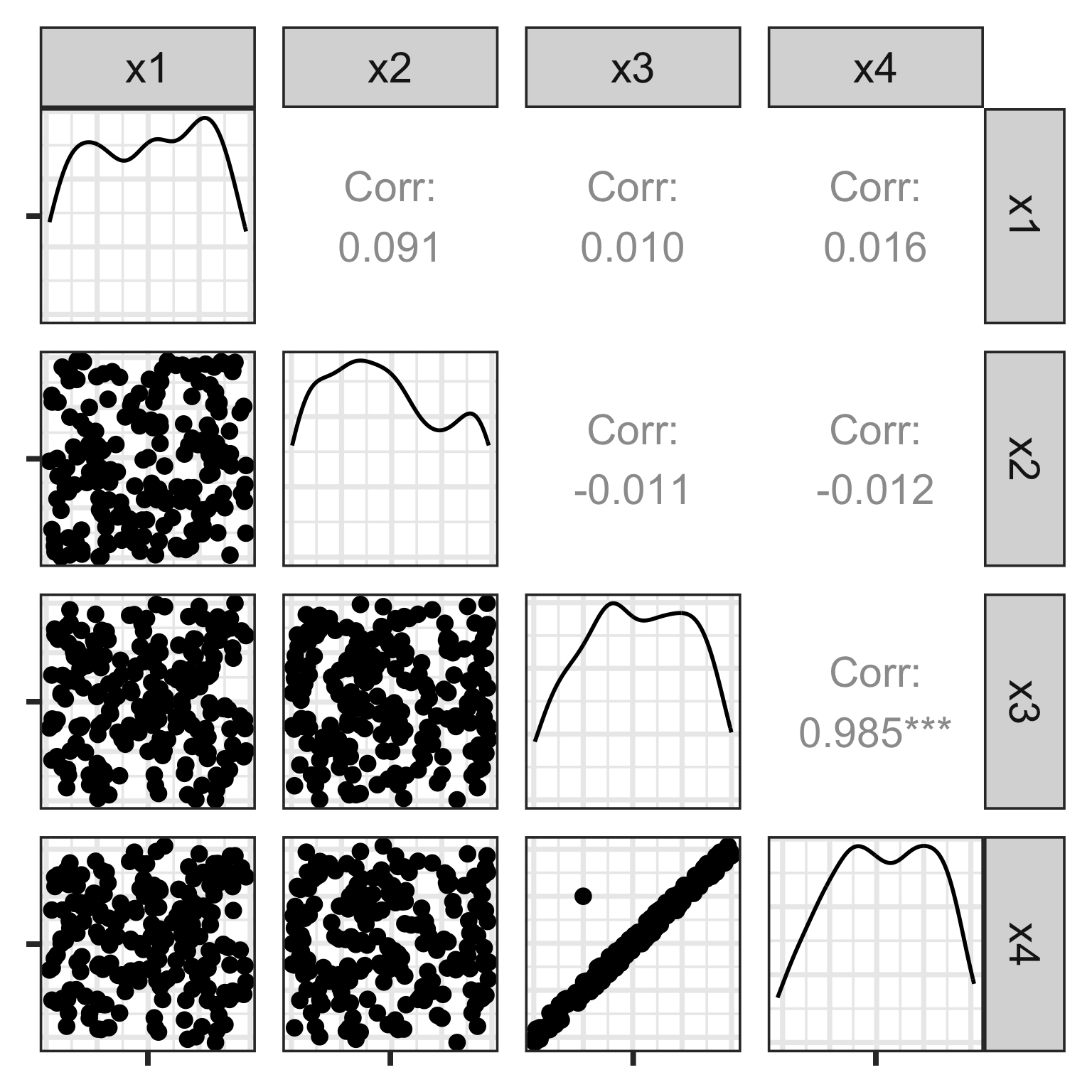
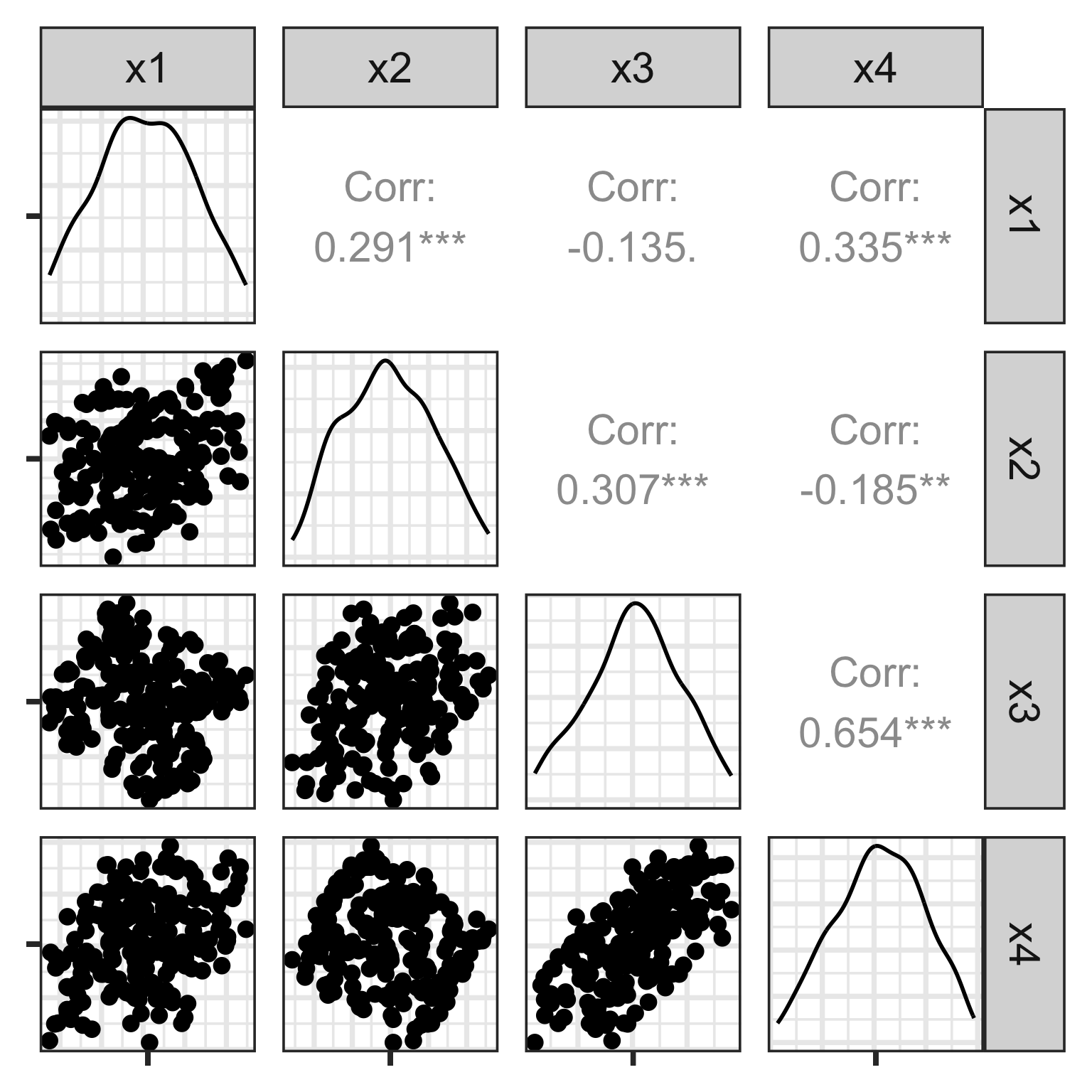
There is an outlier in the data on the right, like the one in the left, but it is hidden in a combination of variables. It’s not visible in any pair of variables.

Perception

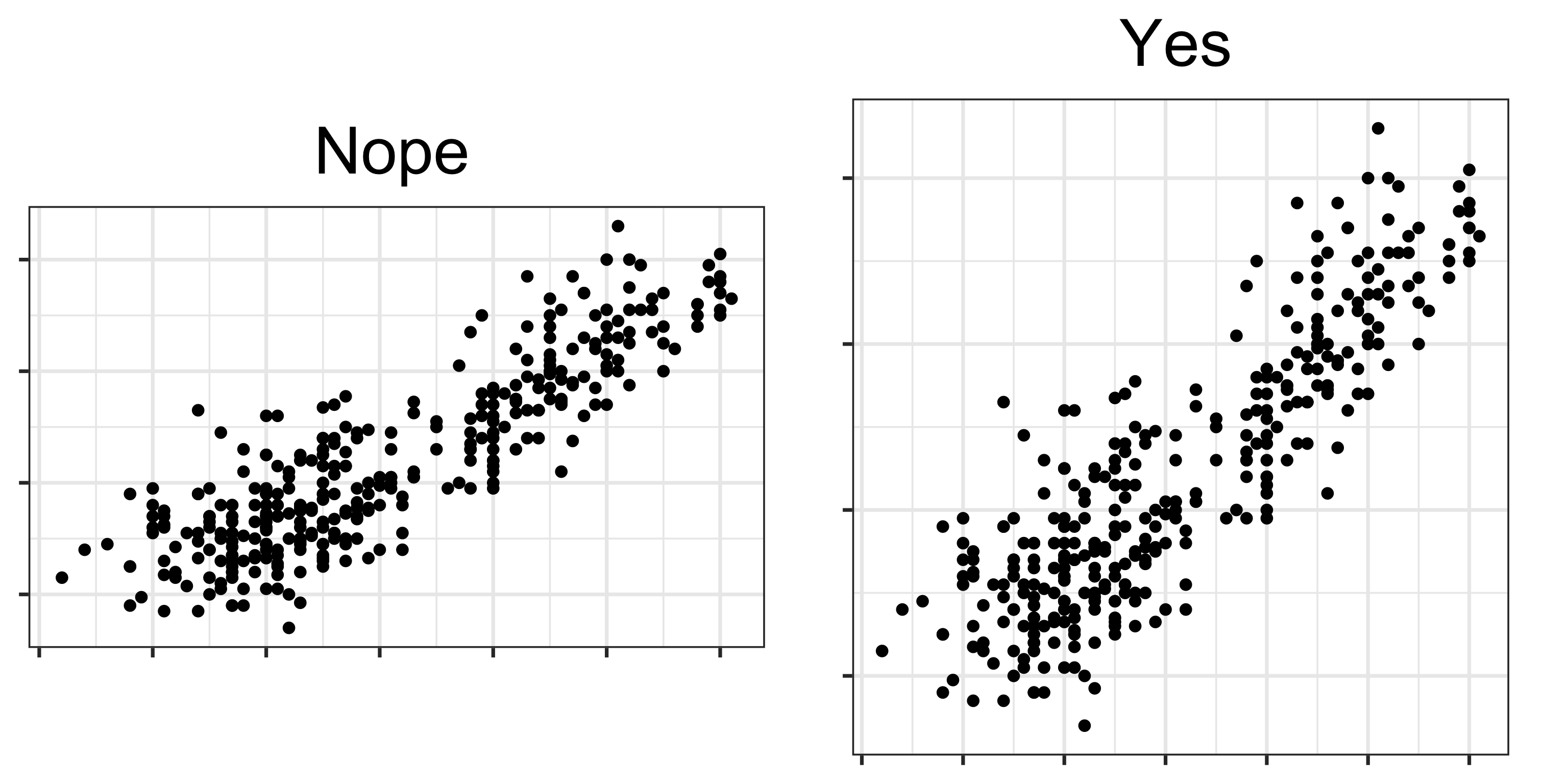
Aspect ratio for scatterplots needs to be equal, or square!

When you make a scatterplot of two variables from a multivariate data set, most software renders it with an unequal aspect ratio, as a rectangle. You need to over-ride this and force the square aspect ratio. Why?

Because it adversely affects the perception of correlation and association between variables.

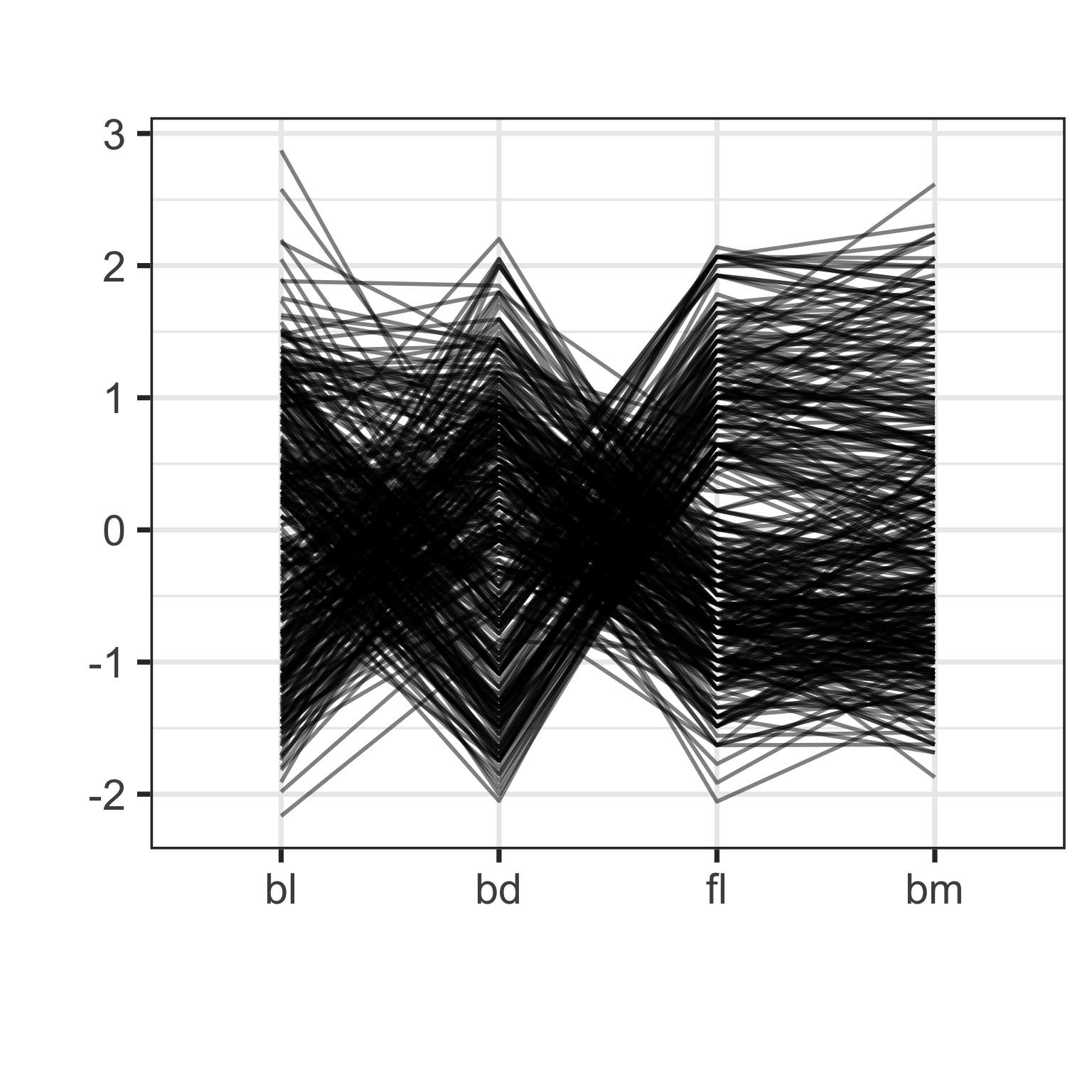
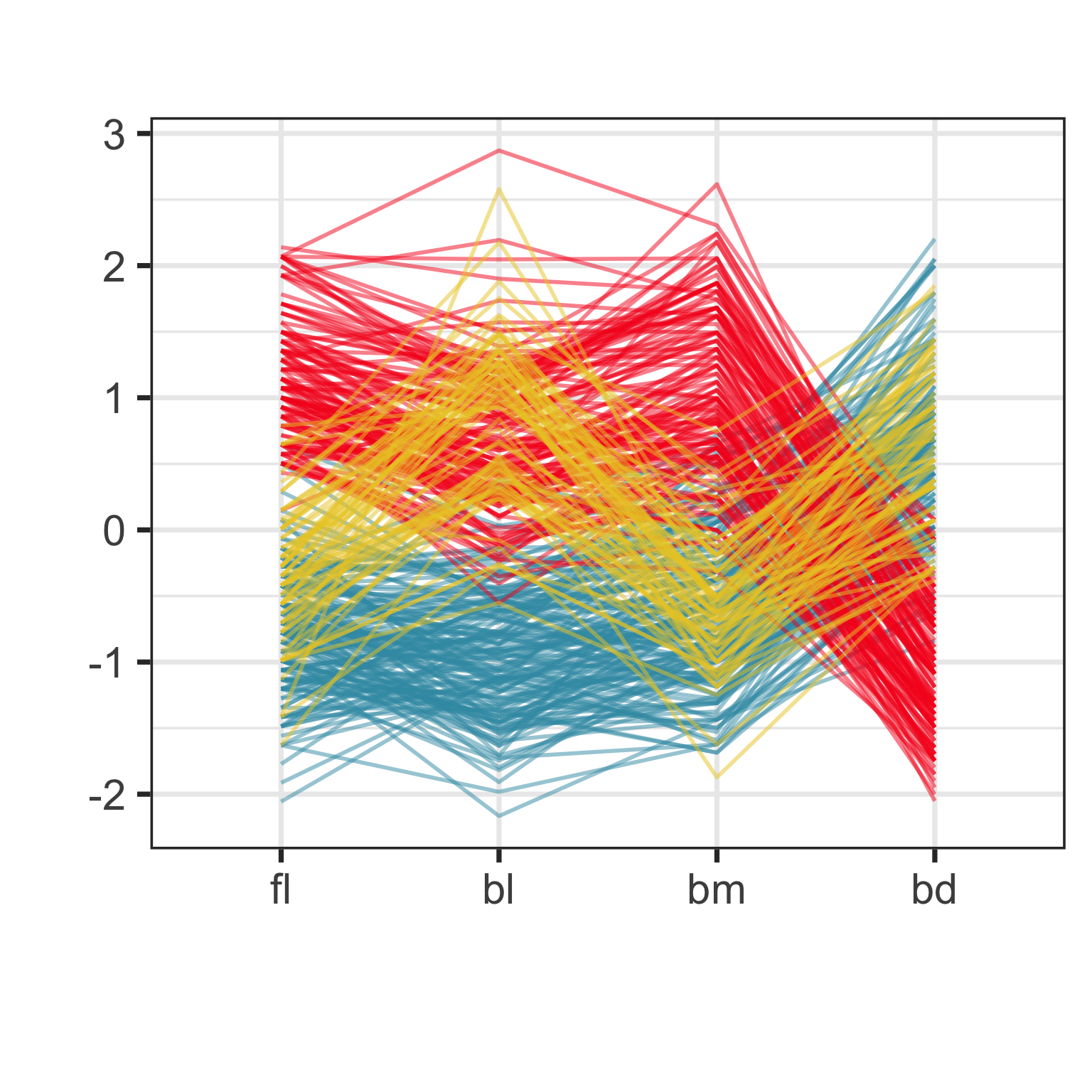
Parallel coordinate plot

ggparcoord(p_tidy, columns = 2:5, alphaLines = 0.5) + 
  xlab("") + ylab("") + 
  theme(aspect.ratio=0.8)

Parallel coordinate plots are side-by-side dotplots with values from a row connected with a line.

Examine the direction and orientation of lines to perceive multivariate relationships.

Crossing lines indicate negative association. Lines with same slope indicate positive association. Outliers have a different up/down pattern to other points. Groups of lines with same pattern indicate clustering.

Parallel coordinate plot: drawbacks

• Hard to follow lines - need interactivity
• Order of variables
• Scaling of variables

But the advantage is that you can pack a lot of variables into the single page.

Parallel coordinate plot: effect of scaling

ggparcoord(p_tidy, columns = 2:5, alphaLines = 0.5,
           scale="globalminmax") + 
  xlab("") + ylab("") + 
  theme(aspect.ratio=0.8)

ggparcoord(p_tidy, columns = 2:5, alphaLines = 0.5,
           scale="uniminmax") + 
  xlab("") + ylab("") + 
  theme(aspect.ratio=0.8)

Parallel coordinate plot: effect of ordering

ggparcoord(p_tidy, columns = 2:5, alphaLines = 0.5,
           groupColumn = 1) + 
  scale_color_discrete_divergingx(palette = "Zissou 1") +
  xlab("") + ylab("") +
  theme(legend.position="none", aspect.ratio=0.8)

ggparcoord(p_tidy, columns = 2:5, alphaLines = 0.5,
           groupColumn = 1, order=c(4, 2, 5, 3)) + 
  scale_color_discrete_divergingx(palette = "Zissou 1") +
  xlab("") + ylab("") +
  theme(legend.position="none", aspect.ratio=0.8)

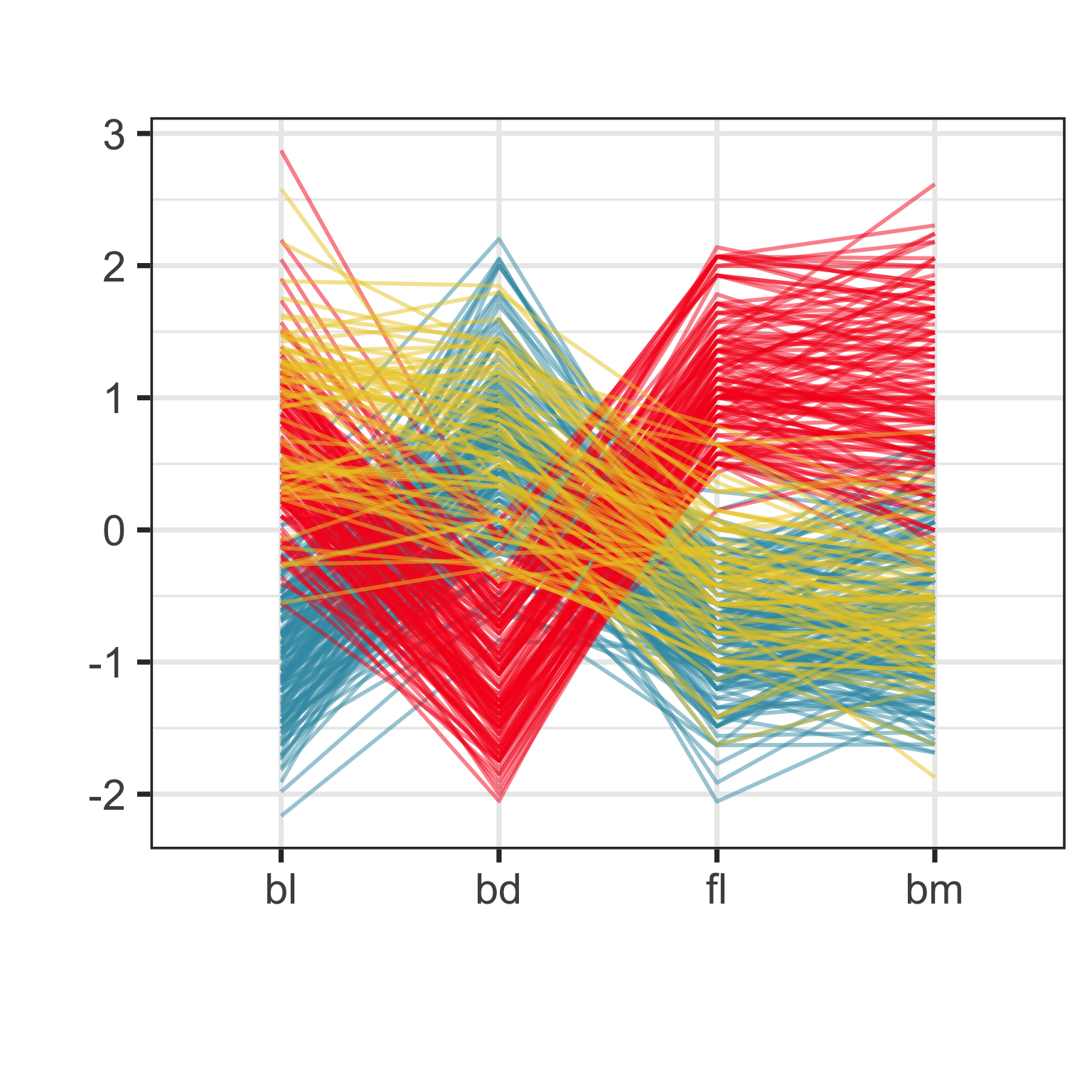
Adding interactivity to static plots: scatterplot matrix

library(plotly)
g <- ggpairs(p_tidy, columns=2:5) +
  theme(axis.text = element_blank()) 

Selecting points, using plotly, allows you to see where this observation lies in the other plots (pairs of variables).

ggplotly(g, width=600, height=600)

Adding interactivity to static plots: parallel coordinates

p_pcp <- p_tidy |>
  na.omit() |>
  plot_ly(type = 'parcoords',
          line = list(),
          dimensions = list(
            list(range = c(172, 231),
                 label = 'fl', values = ~fl),
            list(range = c(32, 60),
                 label = 'bl', values = ~bl),
           list(range = c(2700, 6300),
                 label = 'bm', values = ~bm),
            list(range = c(13, 22),
                 label = 'bd', values = ~bd)
             )
          )

p_pcp

What is high-dimensions?

High-dimensions in statistics

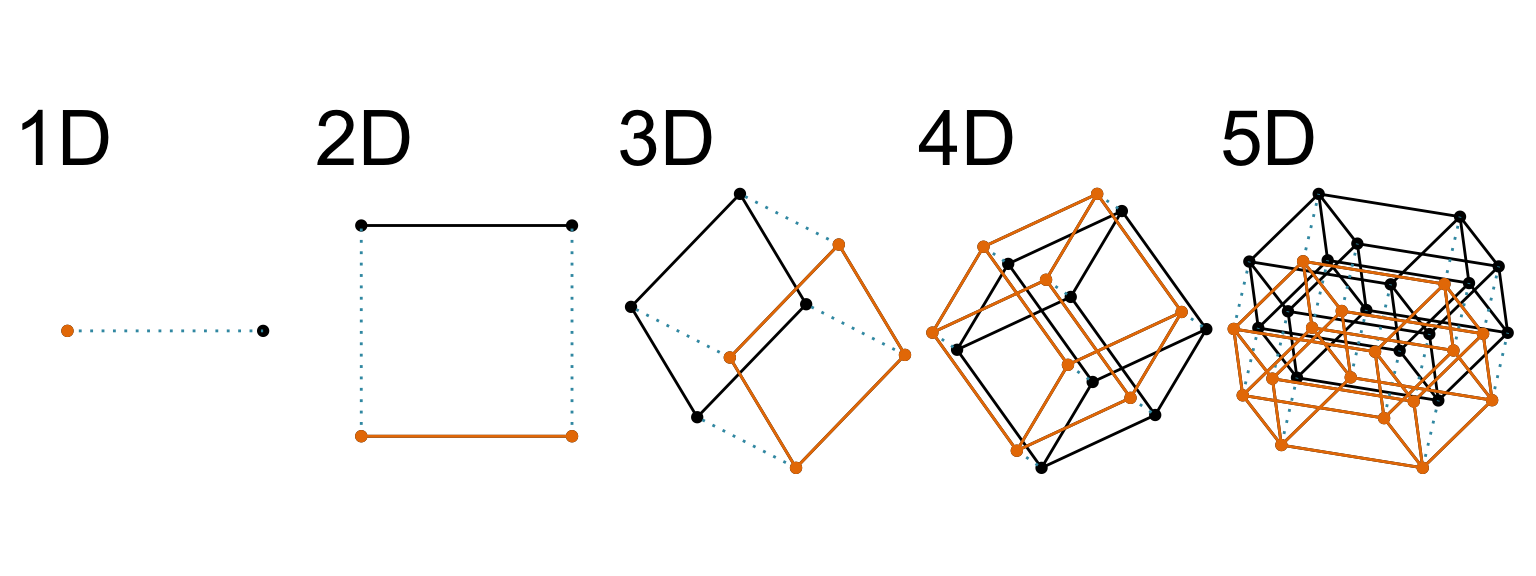
Increasing dimension adds an additional orthogonal axis.

If you want more high-dimensional shapes there is an R package, geozoo, which will generate cubes, spheres, simplices, mobius strips, torii, boy surface, klein bottles, cones, various polytopes, …

And read or watch Flatland: A Romance of Many Dimensions (1884) Edwin Abbott.

Remember

Data

\[\begin{eqnarray*} X_{~n\times p} = [X_{~1}~X_{~2}~\dots~X_{~p}]_{~n\times p} = \left[ \begin{array}{cccc} x_{~11} & x_{~12} & \dots & x_{~1p} \\ x_{~21} & x_{~22} & \dots & x_{~2p}\\ \vdots & \vdots & & \vdots \\ x_{~n1} & x_{~n2} & \dots & x_{~np} \end{array} \right]_{~n\times p} \end{eqnarray*}\]

Remember

Projection

\[\begin{eqnarray*} A_{~p\times d} = \left[ \begin{array}{cccc} a_{~11} & a_{~12} & \dots & a_{~1d} \\ a_{~21} & a_{~22} & \dots & a_{~2d}\\ \vdots & \vdots & & \vdots \\ a_{~p1} & a_{~p2} & \dots & a_{~pd} \end{array} \right]_{~p\times d} \end{eqnarray*}\]

Remember

Projected data

\[\begin{eqnarray*} Y_{~n\times d} = XA = \left[ \begin{array}{cccc} y_{~11} & y_{~12} & \dots & y_{~1d} \\ y_{~21} & y_{~22} & \dots & y_{~2d}\\ \vdots & \vdots & & \vdots \\ y_{~n1} & y_{~n2} & \dots & y_{~nd} \end{array} \right]_{~n\times d} \end{eqnarray*}\]

Tours of linear projections

Data is 2D: \(~~p=2\)

Projection is 1D: \(~~d=1\)

\[\begin{eqnarray*} A_{~2\times 1} = \left[ \begin{array}{c} a_{~11} \\ a_{~21}\\ \end{array} \right]_{~2\times 1} \end{eqnarray*}\]

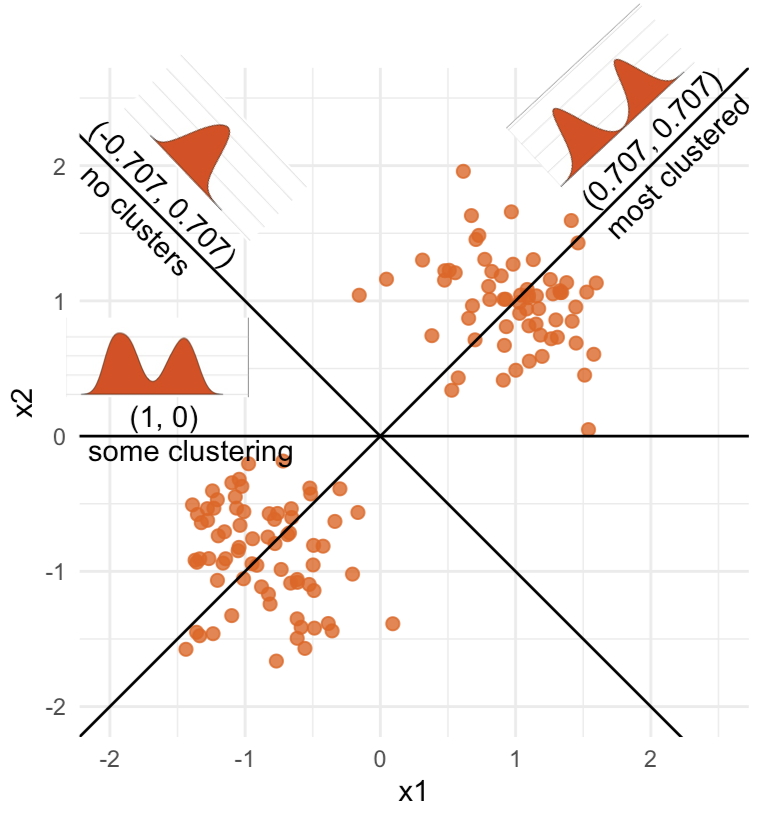
Notice that the values of \(A\) change between (-1, 1). All possible values being shown during the tour.

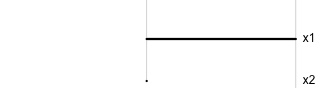
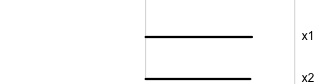
\[\begin{eqnarray*} A = \left[ \begin{array}{c} 1 \\ 0\\ \end{array} \right] ~~~~~~~~~~~~~~~~ A = \left[ \begin{array}{c} 0.7 \\ 0.7\\ \end{array} \right] ~~~~~~~~~~~~~~~~ A = \left[ \begin{array}{c} 0.7 \\ -0.7\\ \end{array} \right] \end{eqnarray*}\]

watching the 1D shadows we can see:

• unimodality
• bimodality, there are two clusters.

What does the 2D data look like? Can you sketch it?

Tours of linear projections

⟵
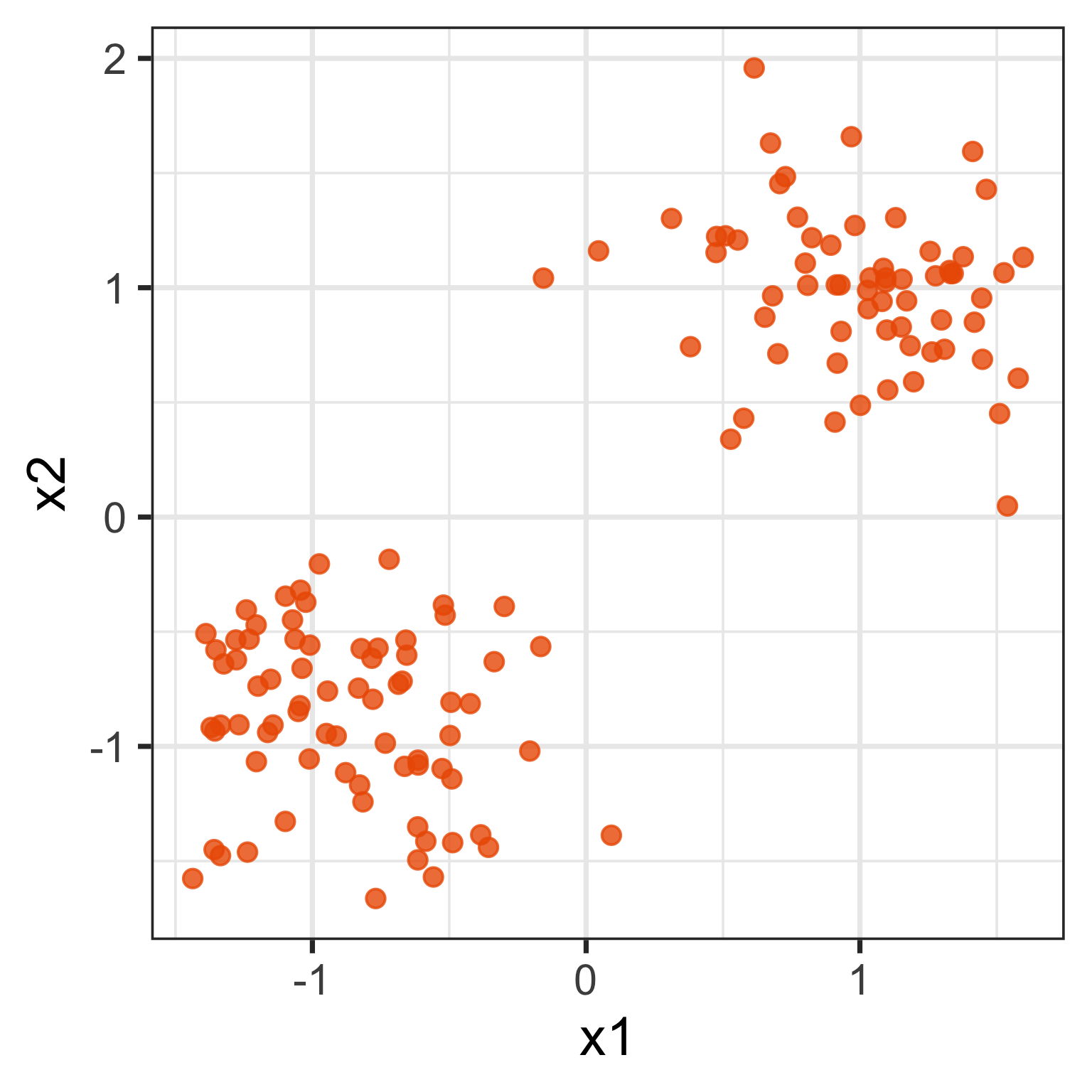
The 2D data

Tours of linear projections

Data is 3D: \(p=3\)

Projection is 2D: \(d=2\)

\[\begin{eqnarray*} A_{~3\times 2} = \left[ \begin{array}{cc} a_{~11} & a_{~12} \\ a_{~21} & a_{~22}\\ a_{~31} & a_{~32}\\ \end{array} \right]_{~3\times 2} \end{eqnarray*}\]

Notice that the values of \(A\) change between (-1, 1). All possible values being shown during the tour.

See:

• circular shapes
• some transparency, reveals middle
• hole in in some projections
• no clustering

Tours of linear projections

Data is 4D: \(p=4\)

Projection is 2D: \(d=2\)

\[\begin{eqnarray*} A_{~4\times 2} = \left[ \begin{array}{cc} a_{~11} & a_{~12} \\ a_{~21} & a_{~22}\\ a_{~31} & a_{~32}\\ a_{~41} & a_{~42}\\ \end{array} \right]_{~4\times 2} \end{eqnarray*}\]

How many clusters do you see?

• three, right?
• one separated, and two very close,
• and they each have an elliptical shape.

• do you also see an outlier or two?

Intuitively, tours are like …

And help to see the data/model as a whole

Avoid misinterpretation …

… see the bigger picture!

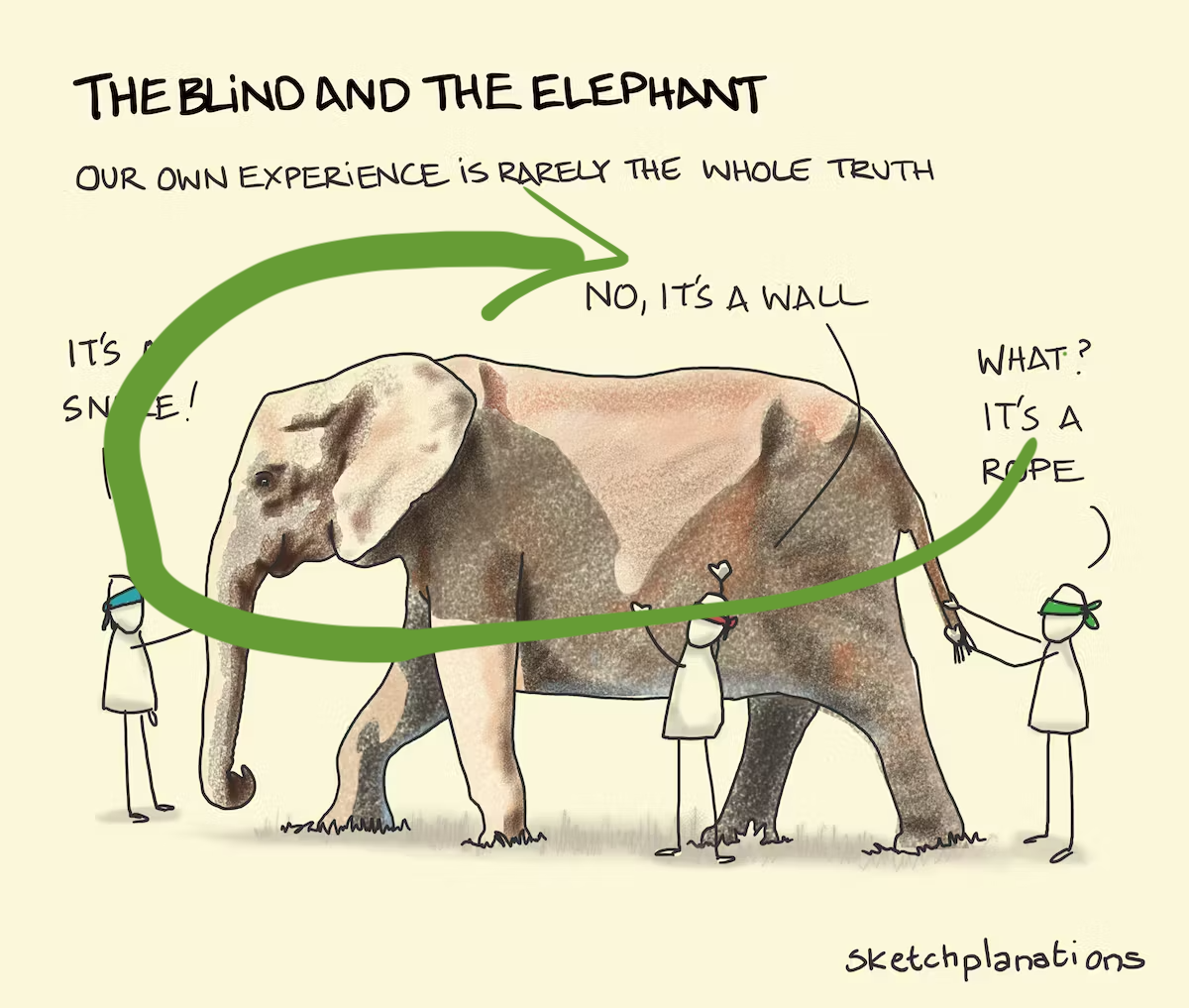
Image: Sketchplanations.

Anomaly is no longer hidden

Wait for it!

How to use a tour in R

This is a basic tour, which will run in your RStudio plot window.

library(tourr)
animate_xy(flea[, 1:6], rescale=TRUE)

This data has a class variable, species.

flea |> slice_head(n=3)

  tars1 tars2  head aede1  aede2 aede3   species
1  0.47  0.83  0.96  1.47 0.9399  0.60 Concinna 
2  0.26  1.18 -0.13  1.18 0.0063  0.67 Concinna 
3  0.77  1.54  0.60  0.89 0.4731  0.46 Concinna 

Use this to colour points with:

animate_xy(flea[, 1:6], 
           col = flea$species, 
           rescale=TRUE)

You can specifically guide the tour choice of projections using

animate_xy(flea[, 1:6], 
           tour_path = guided_tour(holes()), 
           col = flea$species, 
           rescale = TRUE, 
           sphere = TRUE)

and you can manually choose a variable to control with:

set.seed(915)
animate_xy(flea[, 1:6], 
           radial_tour(basis_random(6, 2), 
                       mvar = 6), 
           rescale = TRUE,
           col = flea$species)

How to save a tour

To save as an animated gif:

set.seed(645)
render_gif(penguins_sub[,1:4],
           grand_tour(),
           display_xy(col="#EC5C00",
             half_range=3.8, 
             axes="bottomleft", cex=2.5),
           gif_file = "../gifs/penguins1.gif",
           apf = 1/60,
           frames = 1500,
           width = 500, 
           height = 400)

Dimension reduction

PCA

For this 2D data, sketch a line or a direction that if you squashed the data into it would provide most of the information.

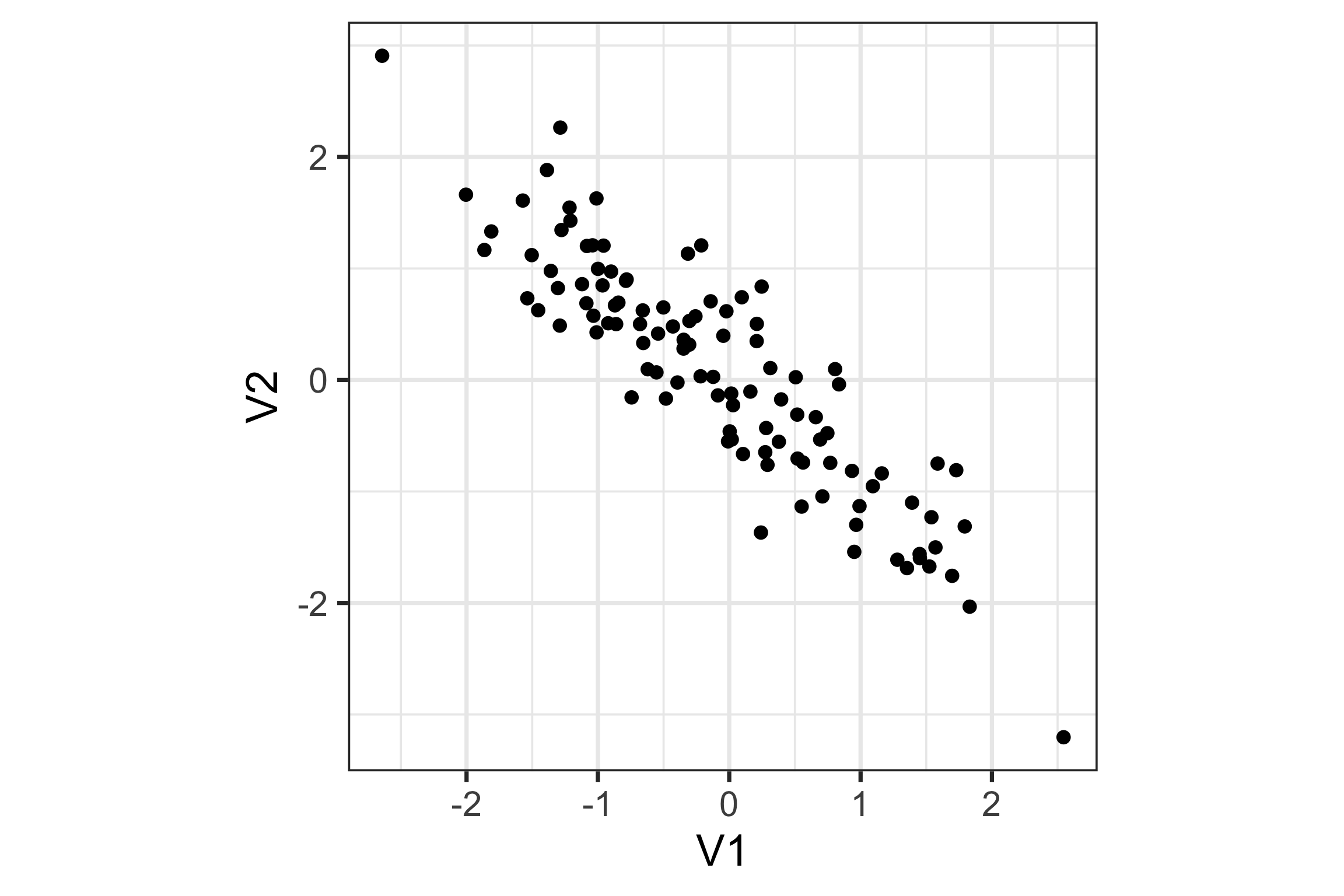
What about this data?

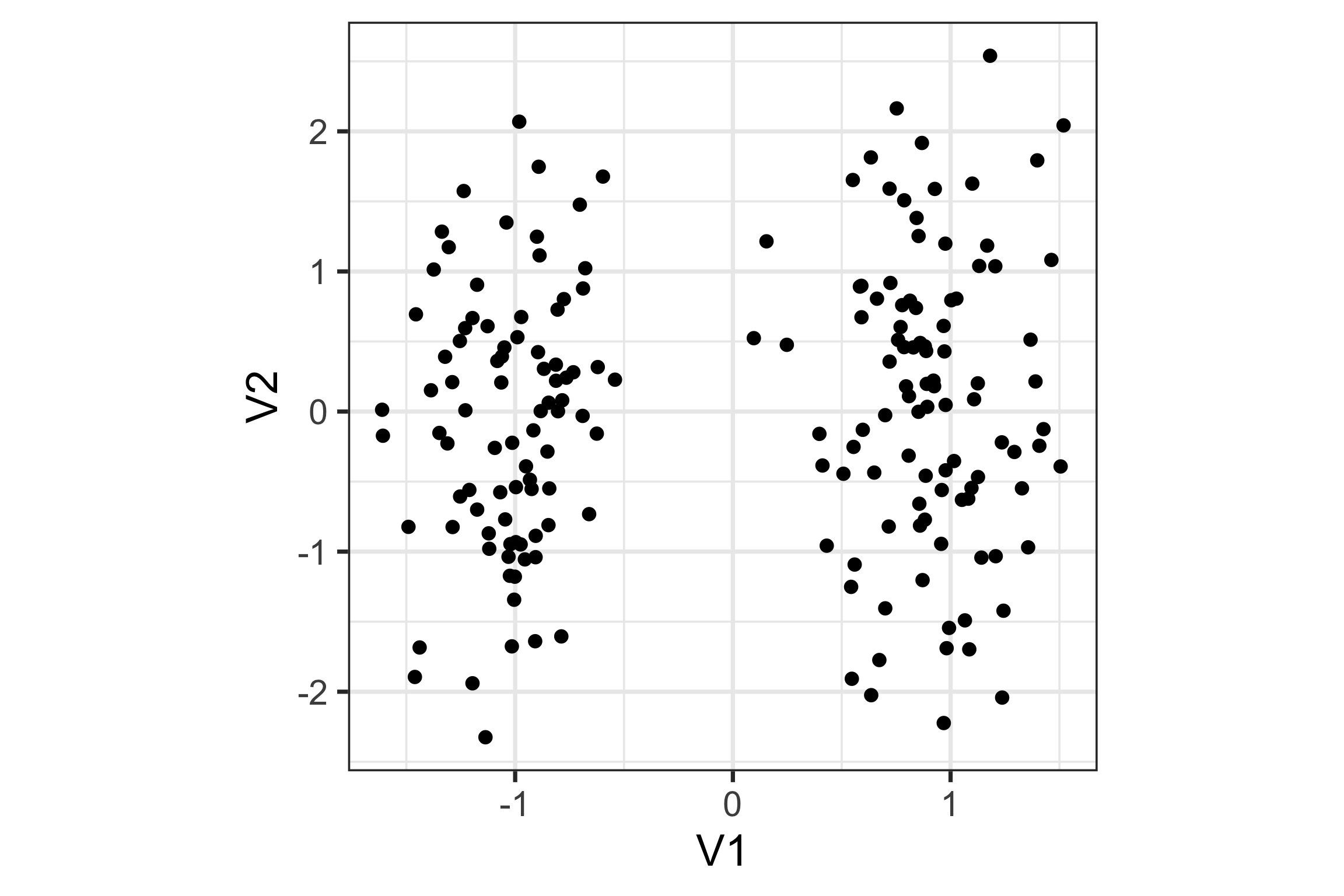
PCA

Principal component analysis (PCA) produces a low-dimensional representation of a dataset. It finds a sequence of linear combinations of the variables that have maximal variance, and are mutually uncorrelated. It is an unsupervised learning method.

Use it, when:

• You have too many predictors for a regression. Instead, we can use the first few principal components.
• Need to understand relationships between variables.
• To make plots summarising the variation in a large number of variables.

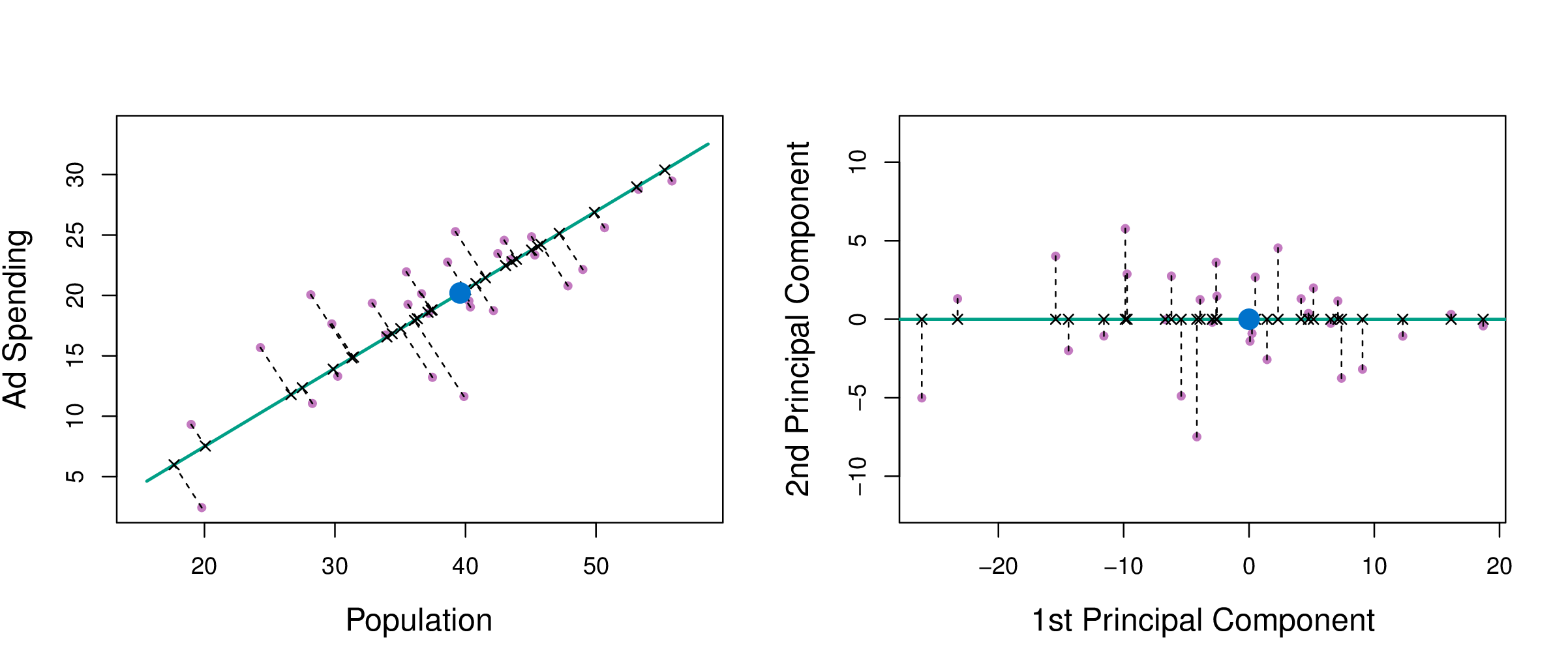
First principal component

The first principal component is a new variable created from a linear combination

\[z_1 = \phi_{11}x_1 + \phi_{21} x_2 + \dots + \phi_{p1} x_p\]

of the original \(x_1, x_2, \dots, x_p\) that has the largest variance. The elements \(\phi_{11},\dots,\phi_{p1}\) are the loadings of the first principal component and are constrained by:

\[ \displaystyle\sum_{j=1}^p \phi^2_{j1} = 1 \]

Calculation

• The loading vector \(\phi_1 = [\phi_{11},\dots,\phi_{p1}]^\top\) defines direction in feature space along which data vary most.
• If we project the \(n\) data points \({x}_1,\dots,{x}_n\) onto this direction, the projected values are the principal component scores \(z_{11},\dots,z_{n1}\).

• The second principal component is the linear combination \(z_{i2} = \phi_{12}x_{i1} + \phi_{22}x_{i2} + \dots + \phi_{p2}x_{ip}\) that has maximal variance among all linear combinations that are uncorrelated with \(z_1\).
• Equivalent to constraining \(\phi_2\) to be orthogonal (perpendicular) to \(\phi_1\). And so on.
• There are at most \(\min(n - 1, p)\) PCs.

Example

If you think of the first few PCs like a linear model fit, and the others as the error, it is like regression, except that errors are orthogonal to model.

(Chapter6/6.15.pdf)

Geometry

PCA can be thought of as fitting an \(n\)-dimensional ellipsoid to the data, where each axis of the ellipsoid represents a principal component. The new variables produced by principal components correspond to rotating and scaling the ellipse into a circle. It spheres the data.

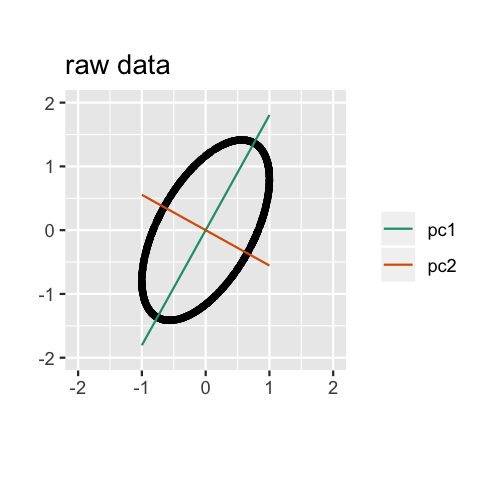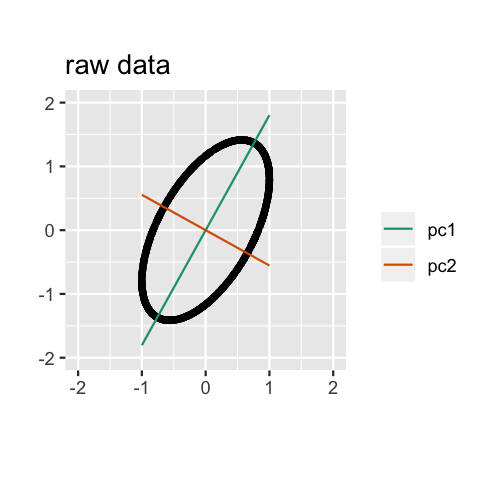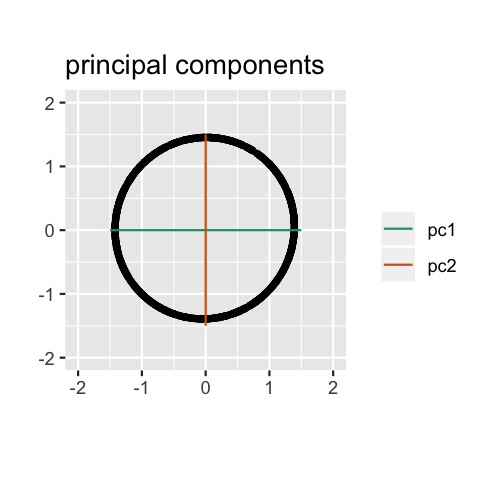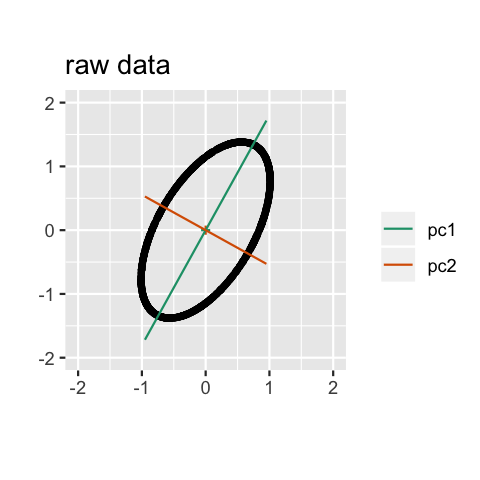
Computation

Suppose we have a \(n\times p\) data set \(X = [x_{ij}]\).

1. Centre each of the variables to have mean zero (i.e., the column means of \({X}\) are zero).
2. Let \(z_{i1} = \phi_{11}x_{i1} + \phi_{21} x_{i2} + \dots + \phi_{p1} x_{ip}\)
3. Compute sample variance of \(z_{i1}\) is \(\displaystyle\frac1n\sum_{i=1}^n z_{i1}^2\).
4. Estimate \(\phi_{j1}\)

\[ \mathop{\text{maximize}}_{\phi_{11},\dots,\phi_{p1}} \frac{1}{n}\sum_{i=1}^n \left(\sum_{j=1}^p \phi_{j1}x_{ij}\right)^{\!\!\!2} \text{ subject to } \sum_{j=1}^p \phi^2_{j1} = 1 \]

Repeat optimisation to estimate \(\phi_{jk}\), with additional constraint that \(\sum_{j=1, k<k'}^p \phi_{jk}\phi_{jk'} = 0\) (next vector is orthogonal to previous eigenvector).

Alternative forumulations

Eigen-decomposition

1. Compute the covariance matrix (after centering the columns of \({X}\)) \[S = {X}^T{X}\]
2. Find eigenvalues (diagonal elements of \(D\)) and eigenvectors ( \(V\) ): \[{S}={V}{D}{V}^T\] where columns of \({V}\) are orthonormal (i.e., \({V}^T{V}={I}\))

Singular Value Decomposition

\[X = U\Lambda V^T\]

• \(X\) is an \(n\times p\) matrix
• \(U\) is \(n \times r\) matrix with orthonormal columns ( \(U^TU=I\) )
• \(\Lambda\) is \(r \times r\) diagonal matrix with non-negative elements. (Square root of the eigenvalues.)
• \(V\) is \(p \times r\) matrix with orthonormal columns (These are the eigenvectors, and \(V^TV=I\) ).

It is always possible to uniquely decompose a matrix in this way.

Total variance

Remember, PCA is trying to summarise the variance in the data.

Total variance (TV) in data (assuming variables centered at 0):

\[ \text{TV} = \sum_{j=1}^p \text{Var}(x_j) = \sum_{j=1}^p \frac{1}{n}\sum_{i=1}^n x_{ij}^2 \]

If variables are standardised, TV=number of variables.

Variance explained by m’th PC: \(V_m = \text{Var}(z_m) = \frac{1}{n}\sum_{i=1}^n z_{im}^2\)

\[ \text{TV} = \sum_{m=1}^M V_m \text{ where }M=\min(n-1,p). \]

How to choose \(k\)?

PCA is a useful dimension reduction technique for large datasets, but deciding on how many dimensions to keep isn’t often clear.

How do we know how many principal components to choose?

How to choose \(k\)?

Proportion of variance explained:

\[\text{PVE}_m = \frac{V_m}{TV}\]

Choosing the number of PCs that adequately summarises the variation in \(X\), is achieved by examining the cumulative proportion of variance explained.

Cumulative proportion of variance explained:

\[\text{CPVE}_k = \sum_{m=1}^k\frac{V_m}{TV}\]

How to choose \(k\)?

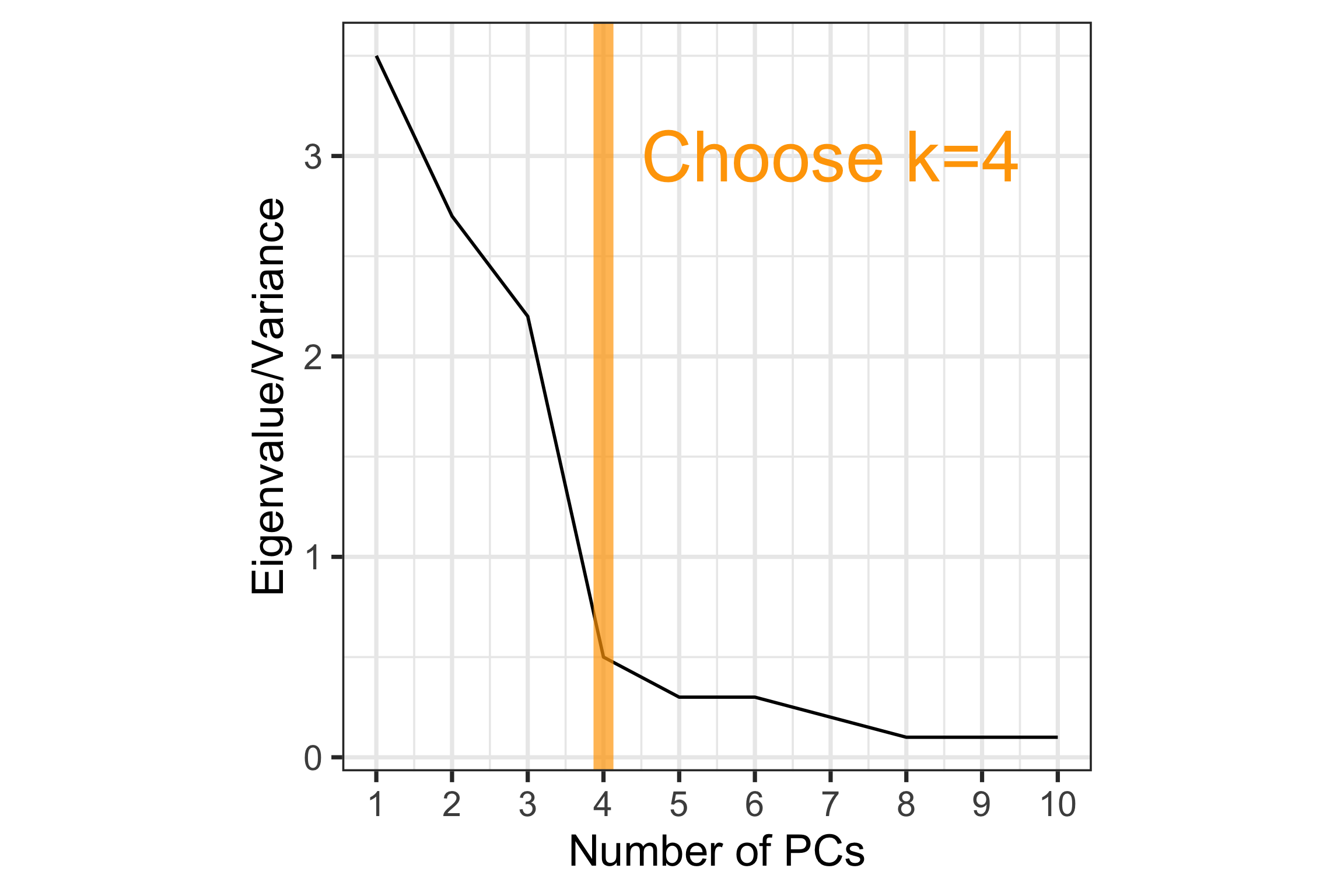
Scree plot: Plot of variance explained by each component vs number of component.

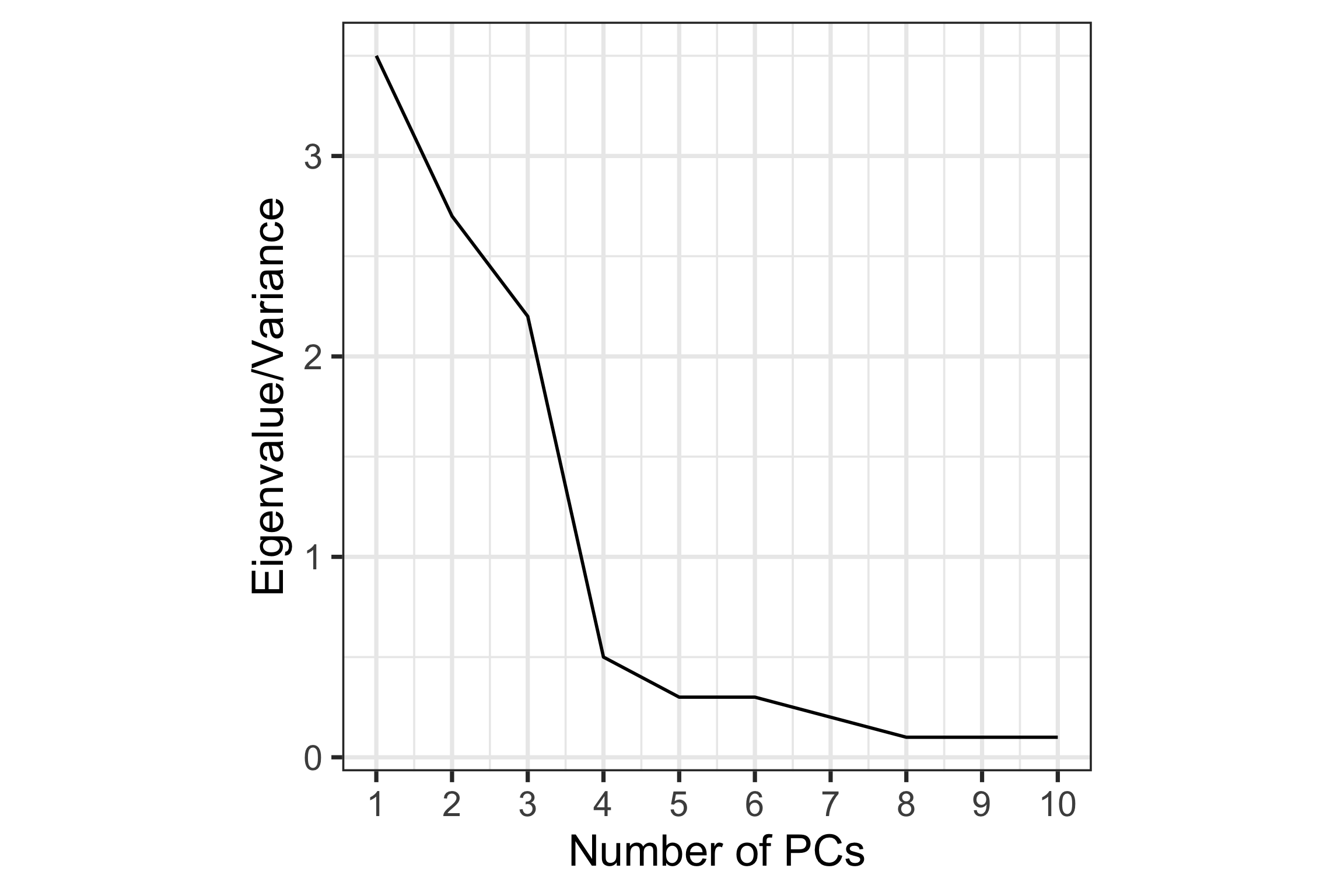
How to choose \(k\)?

Scree plot: Plot of variance explained by each component vs number of component.

Example - track records

The data on national track records for women (as at 1984).

track <- read_csv(here::here("data/womens_track.csv"))
glimpse(track)

Rows: 55
Columns: 8
$ m100     <dbl> 12, 11, 11, 11, 11, 11, 12, 11, 12, 12, 1…
$ m200     <dbl> 23, 22, 23, 23, 23, 23, 24, 22, 25, 24, 2…
$ m400     <dbl> 54, 51, 51, 52, 53, 53, 55, 50, 55, 55, 5…
$ m800     <dbl> 2.1, 2.0, 2.0, 2.0, 2.2, 2.1, 2.2, 2.0, 2…
$ m1500    <dbl> 4.4, 4.1, 4.2, 4.1, 4.6, 4.5, 4.5, 4.1, 4…
$ m3000    <dbl> 9.8, 9.1, 9.3, 8.9, 9.8, 9.8, 9.5, 8.8, 9…
$ marathon <dbl> 179, 152, 159, 158, 170, 169, 191, 149, 1…
$ country  <chr> "argentin", "australi", "austria", "belgi…

Source: Johnson and Wichern, Applied multivariate analysis

Explore the data: scatterplot matrix

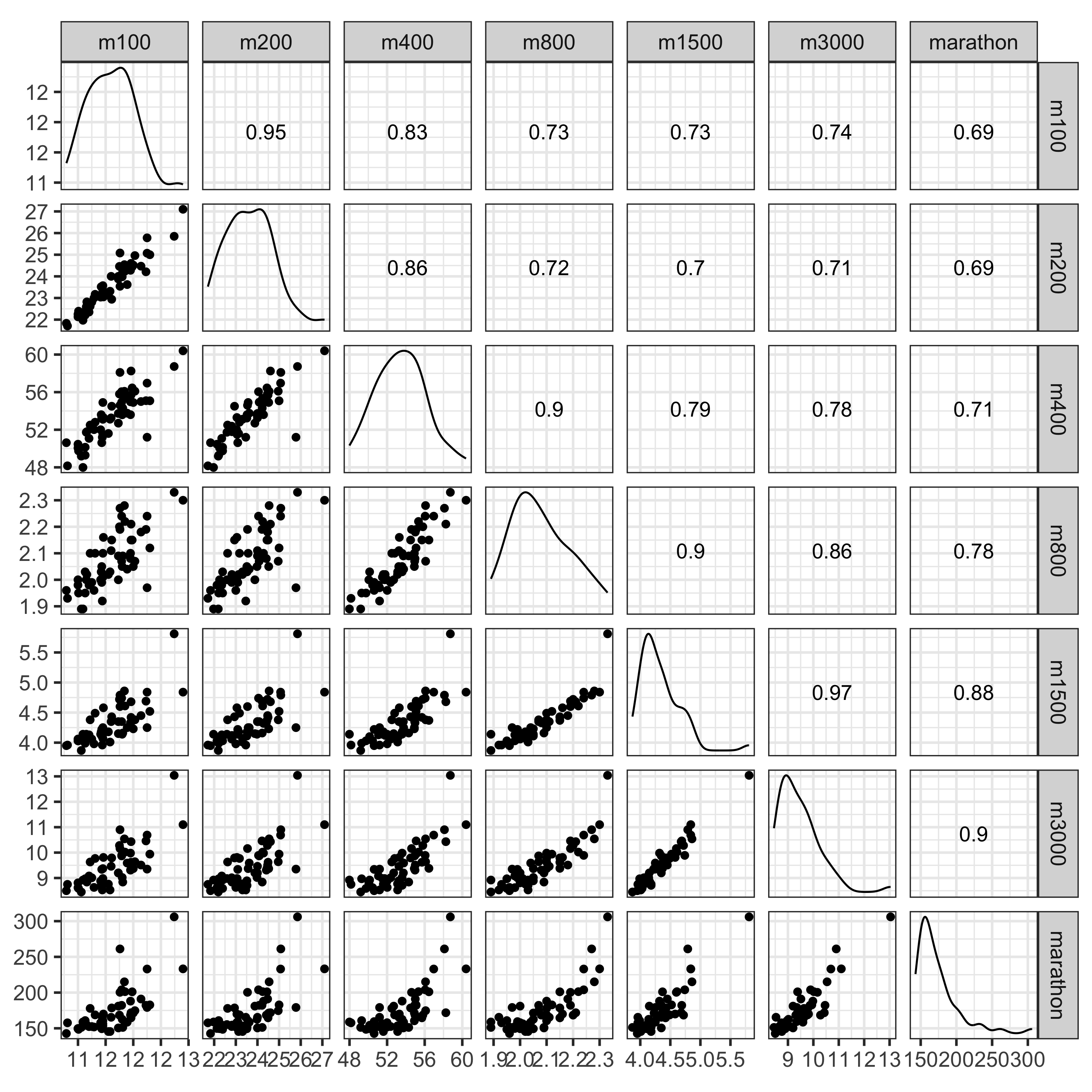
What do you learn?

• Linear relationships between most variables
• Outliers in long distance events, and in 400m vs 100m, 200m
• Non-linear relationship between marathon and 400m, 800m

Explore the data: tour

What do you learn?

• Mostly like a very slightly curved pencil
• Several outliers, in different directions

Compute PCA

options(digits=2)

track_pca <- prcomp(track[,1:7], center=TRUE, scale=TRUE)
track_pca

Standard deviations (1, .., p=7):
[1] 2.41 0.81 0.55 0.35 0.23 0.20 0.15

Rotation (n x k) = (7 x 7):
          PC1   PC2    PC3    PC4    PC5     PC6    PC7
m100     0.37  0.49 -0.286  0.319  0.231  0.6198  0.052
m200     0.37  0.54 -0.230 -0.083  0.041 -0.7108 -0.109
m400     0.38  0.25  0.515 -0.347 -0.572  0.1909  0.208
m800     0.38 -0.16  0.585 -0.042  0.620 -0.0191 -0.315
m1500    0.39 -0.36  0.013  0.430  0.030 -0.2312  0.693
m3000    0.39 -0.35 -0.153  0.363 -0.463  0.0093 -0.598
marathon 0.37 -0.37 -0.484 -0.672  0.131  0.1423  0.070

Summarise

Summary of the principal components:

	PC1	PC2	PC3	PC4	PC5	PC6	PC7
Variance	5.81	0.65	0.30	0.13	0.05	0.04	0.02
Proportion	0.83	0.09	0.04	0.02	0.01	0.01	0.00
Cum. prop	0.83	0.92	0.97	0.98	0.99	1.00	1.00

Increase in variance explained large until \(k=3\) PCs, and then tapers off. A choice of 3 PCs would explain 97% of the total variance.

Decide

Scree plot: Where is the elbow?

At \(k=2\), thus the scree plot suggests 2 PCs would be sufficient to explain the variability.

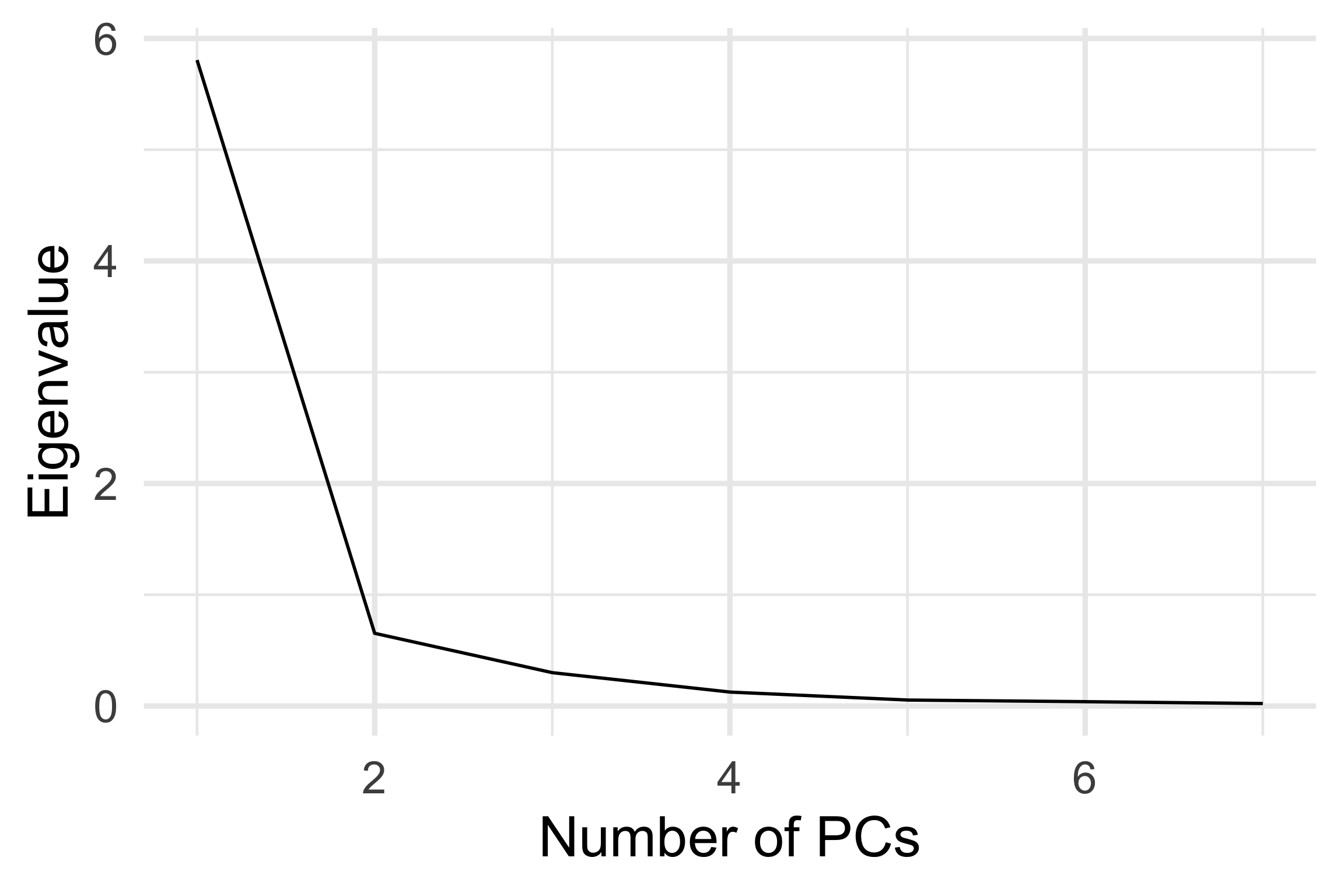
Assess: Data-in-the-model-space

Visualise model using a biplot: Plot the principal component scores, and also the contribution of the original variables to the principal component.

A biplot is like a single projection from a tour.

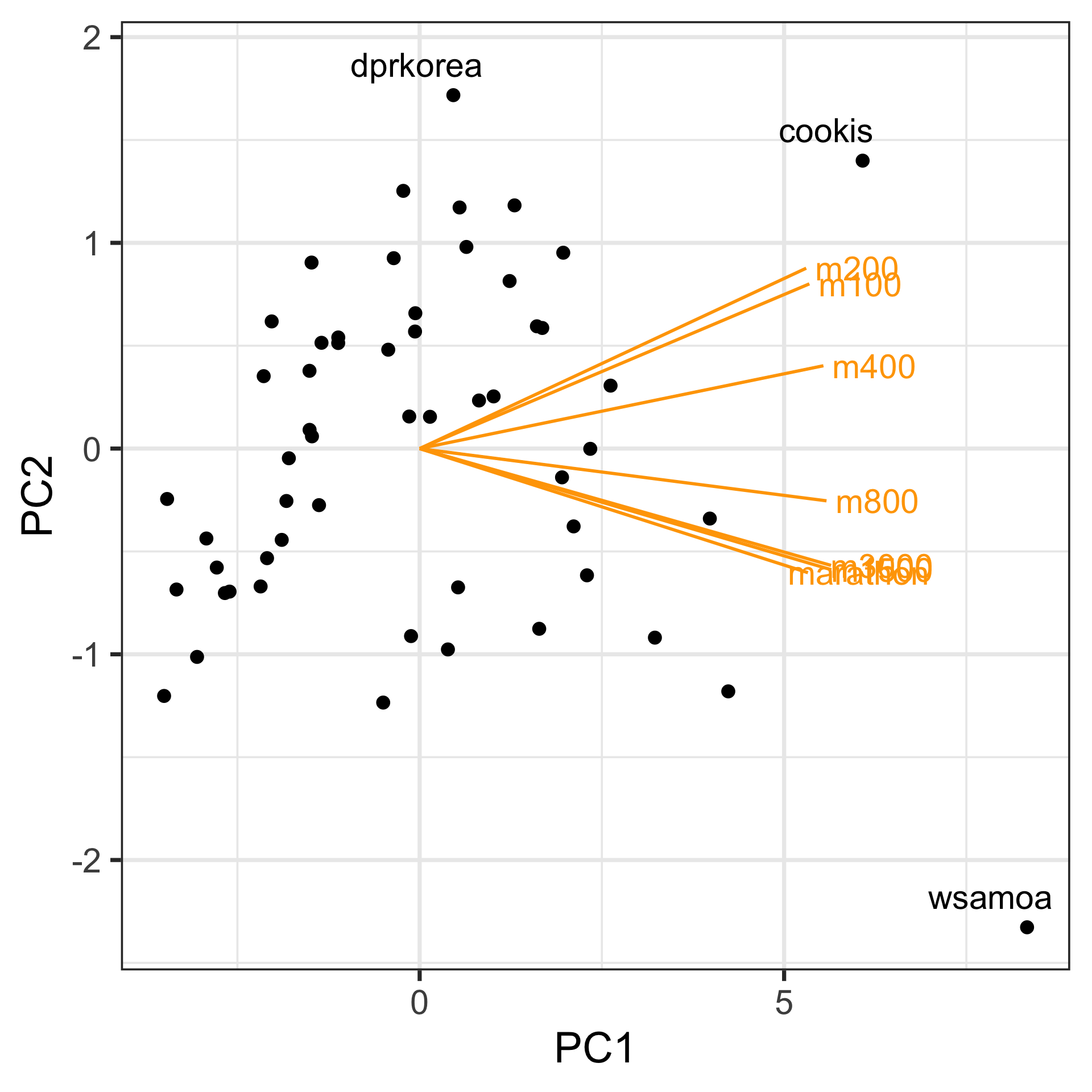
Interpret

• PC1 measures overall magnitude, the strength of the athletics program. High positive values indicate poor programs with generally slow times across events.
• PC2 measures the contrast in the program between short and long distance events. Some countries have relatively stronger long distance atheletes, while others have relatively stronger short distance athletes.
• There are several outliers visible in this plot, wsamoa, cookis, dpkorea. PCA, because it is computed using the variance in the data, can be affected by outliers. It may be better to remove these countries, and re-run the PCA.
• PC3, may or may not be useful to keep. The interpretation would that this variable summarises countries with different middle distance performance.

Assess: Model-in-the-data-space

track_std <- track |>   
  mutate_if(is.numeric, function(x) (x-
      mean(x, na.rm=TRUE))/
      sd(x, na.rm=TRUE))
track_std_pca <- prcomp(track_std[,1:7], 
               scale = FALSE, 
               retx=TRUE)
track_model <- pca_model(track_std_pca, d=2, s=2)
track_all <- rbind(track_model$points, track_std[,1:7])
animate_xy(track_all, edges=track_model$edges,
           edges.col="#E7950F", 
           edges.width=3, 
           axes="off")
render_gif(track_all, 
           grand_tour(), 
           display_xy(
                      edges=track_model$edges, 
                      edges.col="#E7950F", 
                      edges.width=3, 
                      axes="off"),
           gif_file="gifs/track_model.gif",
           frames=500,
           width=400,
           height=400,
           loop=FALSE)

Mostly captures the variance in the data. Seems to slightly miss the non-linear relationship.

Delectable details

🤭

Sometimes the lowest PCs show the interesting patterns, like non-linear relationships, or clusters.

• PCA summarises linear relationships, and might not see other interesting dependencies. Projection pursuit is a generalisation that can find other interesting patterns.
• Outliers can affect results, because direction of outliers will appear to have larger variance
• Scaling of variables matters, and typically you would first standardise each variable to have mean 0 and variance 1. Otherwise, PCA might simply report the variables with the largest variance, which we already know.

Non-linear dimension reduction

Common approaches

Find some low-dimensional layout of points which approximates the distance between points in high-dimensions, with the purpose being to have a useful representation that reveals high-dimensional patterns, like clusters.

Multidimensional scaling (MDS) is the original approach:

\[ \mbox{Stress}_D(x_1, ..., x_n) = \left(\sum_{i, j=1; i\neq j}^n (d_{ij} - d_k(i,j))^2\right)^{1/2} \] where \(D\) is an \(n\times n\) matrix of distances \((d_{ij})\) between all pairs of points, and \(d_k(i,j)\) is the distance between the points in the low-dimensional space.

PCA is a special case of MDS. The result from PCA is a linear projection, but generally MDS can provide some non-linear transformation.

Many variations being developed:

• t-stochastic neighbourhood embedding (t-SNE): compares interpoint distances with a standard probability distribution (eg \(t\)-distribution) to exaggerate local neighbourhood differences.
• uniform manifold approximation and projection (UMAP): compares the interpoint distances with what might be expected if the data was uniformly distributed in the high-dimensions.

NLDR can be useful but it can also make some misleading representations.

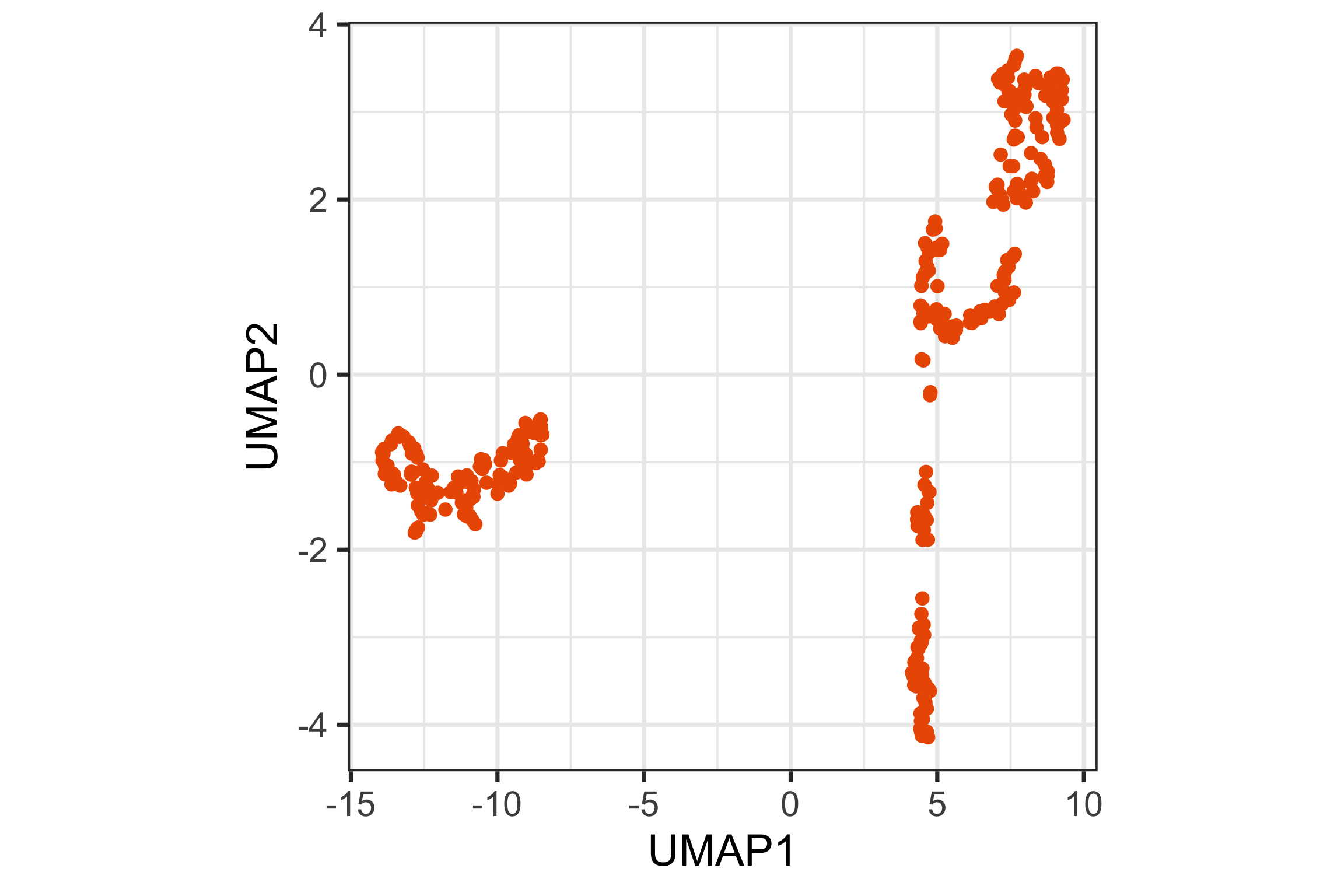
UMAP (1/2)

UMAP 2D representation

library(uwot)
set.seed(253)
p_tidy_umap <- umap(p_tidy_std[,2:5], init = "spca")

Tour animation

UMAP (2/2)

UMAP 2D representation

Tour animation

Next: Re-sampling and regularisation